题目内容
函数y=sinx+cosx+
的最大值等于 ,最小值等于 .
| 1 | ||
|
考点:三角函数的最值
专题:三角函数的求值
分析:令t=sinx+cosx=
sin(x+
)∈[-
,
],分类讨论结合函数的单调性可得答案.
| 2 |
| π |
| 4 |
| 2 |
| 2 |
解答:
解:令t=sinx+cosx=
sin(x+
)∈[-
,
],
当sinx>0,cosx>0时,t∈(0,
],
y=t+
在当t=
时,y取最大值
;
当sinx<0,cosx<0时,t∈[-
,0),
y=t-
在当t=-
时,y取最小值-
;
故答案为:
;-
| 2 |
| π |
| 4 |
| 2 |
| 2 |
当sinx>0,cosx>0时,t∈(0,
| 2 |
y=t+
| 1 |
| t |
| 2 |
3
| ||
| 2 |
当sinx<0,cosx<0时,t∈[-
| 2 |
y=t-
| 1 |
| t |
| 2 |
| ||
| 2 |
故答案为:
3
| ||
| 2 |
| ||
| 2 |
点评:本题考查三角函数的最值,涉及分类讨论和函数的单调性以及换元法,属中档题.

练习册系列答案
相关题目
集合A={x|-2≤x≤2},B={y|y=
,0≤x≤4},则下列关系正确的是( )
| x |
| A、A⊆∁RB |
| B、B⊆∁RA |
| C、∁RA⊆∁RB |
| D、A∪B=R |
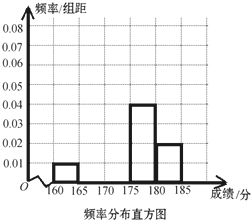 永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示:
永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示: