题目内容
函数f(x)=2x+1+x
的值域是 .
| 1 |
| 2 |
考点:函数的值域
专题:函数的性质及应用
分析:由指数函数和幂函数的单调性得到原函数在定义域内为增函数,由此求得函数的值域.
解答:
解:函数f(x)=2x+1+x
的定义域为[0,+∞),
又函数y1=2x+1在[0,+∞)上为增函数,
函数y2=x
在[0,+∞)上为增函数,
∴函数f(x)=2x+1+x
在[0,+∞)上为增函数,
则当x=0时函数f(x)=2x+1+x
有最小值为20+1+0
=2.
∴函数f(x)=2x+1+x
的值域是[2,+∞).
故答案为:[2,+∞).
| 1 |
| 2 |
又函数y1=2x+1在[0,+∞)上为增函数,
函数y2=x
| 1 |
| 2 |
∴函数f(x)=2x+1+x
| 1 |
| 2 |
则当x=0时函数f(x)=2x+1+x
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)=2x+1+x
| 1 |
| 2 |
故答案为:[2,+∞).
点评:本题考查了指数函数和幂函数的单调性,考查了由函数的单调性求函数的值域,是基础题.

练习册系列答案
相关题目
 某公司试销 一种新产品,规定试销时销售单 价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(图象如图所示).
某公司试销 一种新产品,规定试销时销售单 价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(图象如图所示). 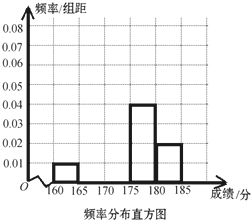 永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示:
永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示: