题目内容
A={y|y=x2-1，x∈R}，B={x∈R|y=
}，则A∩B= ．
| x2-1 |
考点：交集及其运算
专题：集合
分析：利用交集的性质求解．
解答：
解：∵A={y|y=x2-1，x∈R}={y|≥-1}，
B={x∈R|y=
}={x|x2-1≥0}={x|x≥1或x≤-1}，
∴A∩B={x|x≥1或x=-1}．
故答案为：{x|x≥1或x=-1}．
B={x∈R|y=
| x2-1 |
∴A∩B={x|x≥1或x=-1}．
故答案为：{x|x≥1或x=-1}．
点评：本题考查交集的求法，是基础题，解题时要注意函数性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（5
）0.5+（-1）-1÷0.75-2+（2
） -
=（ ）
| 1 |
| 16 |
| 10 |
| 27 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
使（3-2x-x2） -
有意义的x的取值范围是（ ）
| 3 |
| 4 |
| A、R |
| B、x≠1且x≠3 |
| C、-3＜x＜1 |
| D、x＜-3或x＞1 |
在等差数列{an}中，若a4+a6+a8+a10+a12=90，则a10-
a14的值为（ ）
| 1 |
| 3 |
| A、12 | B、14 | C、16 | D、18 |
设集合M={x|4-x2＞0}，N={x∈R||x-1|≤2}，则M∩N等于（ ）
| A、{x|-2＜x≤3} |
| B、{x|-1≤x＜2} |
| C、{x|-2＜x≤-1} |
| D、{x|-1＜x＜2} |
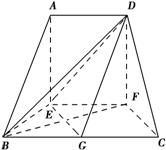在如图的多面体中，AE⊥底面BEFC，AD∥EF∥BC，BE=AD=EF=