题目内容
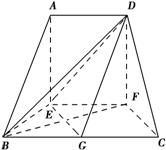 在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=
在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=| 1 |
| 2 |
(1)求证:AB∥平面DEG;
(2)求证:平面EGD⊥平面BDF.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)先证明四边形ADGB是平行四边形,可得AB∥DG,从而证明AB∥平面DEG.
(2)连接GF,可证得四边形BGFE为菱形,进而BF⊥EG,由AE⊥底面BEFC,可得DF⊥EG,由线面垂直的判定定理可得:EG⊥平面BDF,再由面面垂直的判定定理,可得平面EGD⊥平面BDF.
(2)连接GF,可证得四边形BGFE为菱形,进而BF⊥EG,由AE⊥底面BEFC,可得DF⊥EG,由线面垂直的判定定理可得:EG⊥平面BDF,再由面面垂直的判定定理,可得平面EGD⊥平面BDF.
解答:
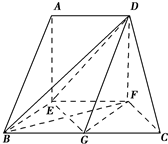 证明:(1)∵AD∥EF,EF∥BC,
证明:(1)∵AD∥EF,EF∥BC,
∴AD∥BC.
又∵BC=2AD,G是BC的中点,
∴AD=BG,
∴四边形ADGB是平行四边形,
∴AB∥DG.
∵AB?平面DEG,DG?平面DEG,
∴AB∥平面DEG.
(2)连接GF,四边形ADFE是矩形,
∵DF∥AE,AE⊥底面BEFC,
∴DF⊥平面BCFE,
又∵EG?平面BCFE,
∴DF⊥EG.
∵EF=BG,EF∥BG,EF=BE,
∴四边形BGFE为菱形,
∴BF⊥EG,
又BF∩DF=F,BF?平面BFD,DF?平面BFD,
∴EG⊥平面BDF.
∵EG?平面EGD,
∴平面EGD⊥平面BDF.
 证明:(1)∵AD∥EF,EF∥BC,
证明:(1)∵AD∥EF,EF∥BC,∴AD∥BC.
又∵BC=2AD,G是BC的中点,
∴AD=BG,
∴四边形ADGB是平行四边形,
∴AB∥DG.
∵AB?平面DEG,DG?平面DEG,
∴AB∥平面DEG.
(2)连接GF,四边形ADFE是矩形,
∵DF∥AE,AE⊥底面BEFC,
∴DF⊥平面BCFE,
又∵EG?平面BCFE,
∴DF⊥EG.
∵EF=BG,EF∥BG,EF=BE,
∴四边形BGFE为菱形,
∴BF⊥EG,
又BF∩DF=F,BF?平面BFD,DF?平面BFD,
∴EG⊥平面BDF.
∵EG?平面EGD,
∴平面EGD⊥平面BDF.
点评:本题考查证明线面平行、面面垂直的方法,考查学生的空间想象能力,属中档题.

练习册系列答案
相关题目
命题“?x∈(0,+∞),2x>1”的否定是( )
| A、?x0∉(0,+∞),2x0≤1 |
| B、?x0∈(0,+∞),2x0≤1 |
| C、?x∉(0,+∞),2x≤1 |
| D、?x∈(0,+∞),2x<1 |
f(x)=
的定义域为( )
(
| ||
|
| A、(0,1]∪(1,2] |
| B、[0,1)∪(1,2) |
| C、[0,1)∪(1,2] |
| D、[0,2) |
函数f(x)=2x+lnx-3的零点位于区间( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |