题目内容
袋里装有5个球,每个球都记有1~5中的一个号码,设号码为x的球量为(x2-5x+30)克,这些球以同等的机会(不受质量的影响)从袋里取出.若同时从袋内任意取出两球,则它们质量相等的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:试验发生包含的事件是任取两个球共有C52种等可能的取法,满足条件的事件是它们重量相等,求出符合条件的事件数,最后根据古典概型及其概率计算公式可得到概率.
解答:
解:设两球的号码分别是m、n,
则有m2-5m+30=n2-5n+30.
所以m+n=5.
而5个球中任意取两球的基本事件总数有
=10(种).
符合题意的只有两种,即两球的号码分别是1,4及2,3.
所以P=
=
.
故答案为:
则有m2-5m+30=n2-5n+30.
所以m+n=5.
而5个球中任意取两球的基本事件总数有
| 5×4 |
| 2 |
符合题意的只有两种,即两球的号码分别是1,4及2,3.
所以P=
| 2 |
| 10 |
| 1 |
| 5 |
故答案为:
| 1 |
| 5 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将函数y=5sin3x的图象向左平移π个单位,得到的图象的解析式是( )
A、y=5sin(3x+
| ||
B、y=5sin(3x-
| ||
| C、y=5sin3x | ||
| D、y=-5sin3x |
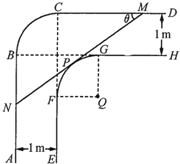 一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m. 在本市某机关今年的公务员考试成绩中随机抽取25名考生的笔试成绩,并分成5组,得到频率分布直方图如图所示.已知成绩落在第2组[110,120)内的人数为8人.
在本市某机关今年的公务员考试成绩中随机抽取25名考生的笔试成绩,并分成5组,得到频率分布直方图如图所示.已知成绩落在第2组[110,120)内的人数为8人.