题目内容
 在本市某机关今年的公务员考试成绩中随机抽取25名考生的笔试成绩,并分成5组,得到频率分布直方图如图所示.已知成绩落在第2组[110,120)内的人数为8人.
在本市某机关今年的公务员考试成绩中随机抽取25名考生的笔试成绩,并分成5组,得到频率分布直方图如图所示.已知成绩落在第2组[110,120)内的人数为8人.(1)求m,n值;
(2)根据直方图估计这25名考生的平均成绩.
考点:频率分布直方图
专题:概率与统计
分析:(1)根据第2组[110,120)内的人数为8人先计算第二组的频率,再由矩形的高=
得到答案,进而根据各组累积频率为1,求出第三,四组的频率及矩形的高n;
(2)数据的平均数是各组组中值与频率乘积的累加值,由已知中的频率分布直方图求出各组组中值及频率,代入可得答案.
| 频率 |
| 组距 |
(2)数据的平均数是各组组中值与频率乘积的累加值,由已知中的频率分布直方图求出各组组中值及频率,代入可得答案.
解答:
解:(1)∵25名考生的笔试成绩中成绩落在第2组[110,120)内的人数为8人,
故第2组[110,120)频率为:
=0.32,
则m=
=0.032,
由已知的频率分布直方图可得:
10×(0.016+0.032+2n+0.012)=1,
解得n=0.020,
(2)由(105×0.016+115×0.032+125×0.020+135×0.020+145×0.012)×10=123,
即这25名考生的平均成绩约为123分.
故第2组[110,120)频率为:
| 8 |
| 25 |
则m=
| 0.32 |
| 10 |
由已知的频率分布直方图可得:
10×(0.016+0.032+2n+0.012)=1,
解得n=0.020,
(2)由(105×0.016+115×0.032+125×0.020+135×0.020+145×0.012)×10=123,
即这25名考生的平均成绩约为123分.
点评:本题考查的知识点是频率分布直方图,其中熟练掌握矩形的高=
,及利用频率分布直方图估算平均数的方法是解答的关键.
| 频率 |
| 组距 |

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
cos20°sin65°-sin20°cos65°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
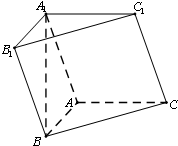 如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.
如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.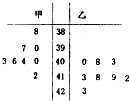 为调查甲乙两人网站受欢迎的程度,随机选取了某个月1号至8号,统计这8天内每天同一时间段的点击量,得到如图所示的茎叶图.
为调查甲乙两人网站受欢迎的程度,随机选取了某个月1号至8号,统计这8天内每天同一时间段的点击量,得到如图所示的茎叶图.