题目内容
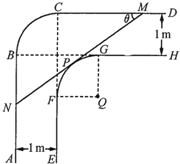 一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.(1)若水平放置的木棒MN的两个端点M,N分别在外壁CD和AB上,且木棒与内壁圆弧相切于点P,设∠CMN=θ,若θ=
| π |
| 4 |
(2)若一根水平放置的木棒能通过该走廊拐角处,请问木棒长度能否大于a,并说明理由.
考点:解三角形的实际应用
专题:解三角形
分析:(1)如设圆弧FG所在的圆的圆心为Q,过Q点作CD的垂线,垂足为点T,且交MN或其延长线于S,并连结PQ,再过点N作TQ的垂线,垂足为W,在Rt△NWS中,由WN和θ表示出NS,因为MN与圆弧FG切于点P,所以PQ⊥MN,进而在Rt△QPS中分别表示出QS,QT-QS,然后对S在TG上,和在线段GT的延长线上,分类讨论,分别表示出MN.
(2)设sinθ+cosθ=t,继而利用三角函数基本关系,表示出设sinθcosθ,f(θ)转换为f(t),进而函数的单调性求得函数的最小值.
(2)设sinθ+cosθ=t,继而利用三角函数基本关系,表示出设sinθcosθ,f(θ)转换为f(t),进而函数的单调性求得函数的最小值.
解答:
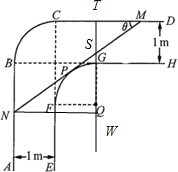 解:(1)如图,设圆弧FG所在的圆的圆心为Q,过Q点作CD的垂线,垂足为点T,且交MN或其延长线于S,并连结PQ,再过点N作TQ的垂线,垂足为W,在Rt△NWS中,因为NW=2,∠SNW=θ,所以NS=
解:(1)如图,设圆弧FG所在的圆的圆心为Q,过Q点作CD的垂线,垂足为点T,且交MN或其延长线于S,并连结PQ,再过点N作TQ的垂线,垂足为W,在Rt△NWS中,因为NW=2,∠SNW=θ,所以NS=
,
因为MN与圆弧FG切于点P,所以PQ⊥MN,在Rt△QPS中,因为PQ=1,∠PQS=θ,所以QS=
,QT-QS=2-
,
①S在线段TG上,则TS=QT-QS,
在Rt△STM中,MS=
=
,
因此MN=NS+MS=NS+
.
②若S在线段GT的延长线上,则TS=QS-QT,在Rt△STM中,
MS=
=
,因此MN=NS-MS=NS-
=NS+
,
f(θ)=MN=NS+
=
+(
-
)=
(0<θ<
),
a=f(
)=
=4
-2
(2)不能大于a.
设sinθ+cosθ=t(1<t≤
)则sinθcosθ=
,因此f(θ)=g(t)=
,
令m=4t-2(2<m≤4
-2),则
=
=
,
当2<m≤4
-2时,上式单调递减,所以g(t)min=4
-2,即MNmin=4
-2.
所以一根水平放置的木棒若能通过该走廊拐角处,则其长度的最大值为4
-2,即不能大于a.
 解:(1)如图,设圆弧FG所在的圆的圆心为Q,过Q点作CD的垂线,垂足为点T,且交MN或其延长线于S,并连结PQ,再过点N作TQ的垂线,垂足为W,在Rt△NWS中,因为NW=2,∠SNW=θ,所以NS=
解:(1)如图,设圆弧FG所在的圆的圆心为Q,过Q点作CD的垂线,垂足为点T,且交MN或其延长线于S,并连结PQ,再过点N作TQ的垂线,垂足为W,在Rt△NWS中,因为NW=2,∠SNW=θ,所以NS=| 2 |
| cosθ |
因为MN与圆弧FG切于点P,所以PQ⊥MN,在Rt△QPS中,因为PQ=1,∠PQS=θ,所以QS=
| 1 |
| cosθ |
| 1 |
| cosθ |
①S在线段TG上,则TS=QT-QS,
在Rt△STM中,MS=
| TS |
| sinθ |
| QT-QS |
| sinθ |
因此MN=NS+MS=NS+
| QT-QS |
| sinθ |
②若S在线段GT的延长线上,则TS=QS-QT,在Rt△STM中,
MS=
| TS |
| sinθ |
| QT-QS |
| sinθ |
| QS-QT |
| sinθ |
| QT-QS |
| sinθ |
f(θ)=MN=NS+
| QT-QS |
| sinθ |
| 2 |
| cosθ |
| 2 |
| sinθ |
| 1 |
| sinθcosθ |
| 2sinθ+2cosθ-1 |
| sinθcosθ |
| π |
| 2 |
a=f(
| π |
| 4 |
2(
| ||||||||
|
| 2 |
(2)不能大于a.
设sinθ+cosθ=t(1<t≤
| 2 |
| t2-1 |
| 2 |
| 4t-2 |
| t2-1 |
令m=4t-2(2<m≤4
| 2 |
| 4t-2 |
| t2-1 |
| 16m |
| m2+4m-12 |
| 16 | ||
m-
|
当2<m≤4
| 2 |
| 2 |
| 2 |
所以一根水平放置的木棒若能通过该走廊拐角处,则其长度的最大值为4
| 2 |
点评:本题主要考查了解三角形问题的实际应用.考查了学生函数思想以及转化与化归的思想.

练习册系列答案
相关题目
若沿△ABC三条边的中位线折起能拼成一个三棱锥,则△ABC( )
| A、一定是等边三角形 |
| B、一定是锐角三角形 |
| C、可以是直角三角形 |
| D、可以是钝角三角形 |
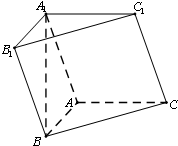 如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.
如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.