题目内容
已知函数f（x）=2cosxsin（x+
）-
sin2x+sinxcosx
（1）证明：f（x）在[-
，
]上递增；
（2）若x∈[0，
]，求f（x）的最大值和最小值．
| π |
| 3 |
| 3 |
（1）证明：f（x）在[-
| π |
| 3 |
| π |
| 12 |
（2）若x∈[0，
| π |
| 2 |
考点：两角和与差的正弦函数,二倍角的余弦,正弦函数的定义域和值域
专题：常规题型,三角函数的图像与性质
分析：（1）利用和差公式及倍角公式化成正弦型函数的标准形式，然后根据正弦函数的单调区间求f（x）的单调区间，进而证明区间[-
，
]是f（x）的单调区间的一个子区间；
（2）根据x的取值范围求出2x+
的范围，然后求出2sin（2x+
）的范围，即可得到f（x）的最大值与最小值．
| π |
| 3 |
| π |
| 12 |
（2）根据x的取值范围求出2x+
| π |
| 3 |
| π |
| 3 |
解答：
解：（1）函数f（x）=2cosxsin（x+
）-
sin2x+sinxcosx
=2cosx（
sinx+
cosx）-
（1-cos2x）+
sin2x
=sinxcosx+
cos2x-
+
cos2x+
sin2x
=sin2x+
cos2x
=2sin（2x+
），
由-
+2kπ≤2x+
≤
+2kπ得：-
+kπ≤x≤
+kπ，（k∈Z）
当k=0时，函数f（x）的一个单调递增区间为[-
，
]，
又∵[-
，
]⊆[-
，
]，
∴f（x）在[-
，
]上递增；
（2）∵x∈[0，
]，∴2x+
∈[
，
]
∴-
≤2sin（2x+
）≤2
∴求f（x）的最大值为2，最小值为-
．
| π |
| 3 |
| 3 |
=2cosx（
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=sinxcosx+
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=sin2x+
| 3 |
=2sin（2x+
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
当k=0时，函数f（x）的一个单调递增区间为[-
| 5π |
| 12 |
| π |
| 12 |
又∵[-
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
∴f（x）在[-
| π |
| 3 |
| π |
| 12 |
（2）∵x∈[0，
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴-
| 3 |
| π |
| 3 |
∴求f（x）的最大值为2，最小值为-
| 3 |
点评：本题考查了三角变换及三角函数的性质，解决本题的关键是把函数表达式化成正弦型函数的标准形式，根据正弦函数的性质研究函数f（x）的性质．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
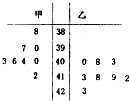为调查甲乙两人网站受欢迎的程度，随机选取了某个月1号至8号，统计这8天内每天同一时间段的点击量，得到如图所示的茎叶图．