题目内容
甲工作室有1名高级工程师A1和3名工程师B1,B2,B3,乙工作室有2名高级工程师A2,A3和1名工程师B4,现要从甲工作室中选出2人,从乙工作室中选出1人支援外地建设.
(Ⅰ)试问:一共有多少种不同的选法?请列出所有可能的选法;
(Ⅱ)求选出的3人均是工程师的概率:
(Ⅲ)求选出的3人中至少有1名高级工程师的概率.
(Ⅰ)试问:一共有多少种不同的选法?请列出所有可能的选法;
(Ⅱ)求选出的3人均是工程师的概率:
(Ⅲ)求选出的3人中至少有1名高级工程师的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(I)要从甲工作室中选出2人,从乙工作室中选出1人,共有
•
=18种不同的选法,按次序列举可得答案;
(II)计算出选出的3人均是工程师的选法种数,代入古典概型概率计算公式,可得答案;
(Ⅲ)选出的3人中至少有1名高级工程师和选出的3人均是工程师互为对立事件,代入对立事件概率减法公式,可得答案.
| C | 2 4 |
| C | 1 3 |
(II)计算出选出的3人均是工程师的选法种数,代入古典概型概率计算公式,可得答案;
(Ⅲ)选出的3人中至少有1名高级工程师和选出的3人均是工程师互为对立事件,代入对立事件概率减法公式,可得答案.
解答:
解:(I)要从甲工作室中选出2人,从乙工作室中选出1人,共有
•
=18种不同的选法,分别为:
(A1,B1,A2),(A1,B1,A3),(A1,B1,B4),(A1,B2,A2),(A1,B2,A3),(A1,B2,B4),
(A1,B3,A2),(A1,B3,A3),(A1,B3,B4),(B1,B2,A2),(B1,B2,A3),(B1,B2,B4),
(B1,B3,A2),(B1,B3,A3),(B1,B3,B4),(B2,B3,A2),(B2,B3,A3),(B2,B3,B4),
(II)其中选出的3人均是工程师选法,共有
•
=3种,分别为:
(B1,B2,B4),(B1,B3,B4),(B2,B3,B4),
故选出的3人均是工程师的概率P=
=
,
(III)选出的3人中至少有1名高级工程师和选出的3人均是工程师互为对立事件,
故选出的3人中至少有1名高级工程师的概率P=1-
=
.
| C | 2 4 |
| C | 1 3 |
(A1,B1,A2),(A1,B1,A3),(A1,B1,B4),(A1,B2,A2),(A1,B2,A3),(A1,B2,B4),
(A1,B3,A2),(A1,B3,A3),(A1,B3,B4),(B1,B2,A2),(B1,B2,A3),(B1,B2,B4),
(B1,B3,A2),(B1,B3,A3),(B1,B3,B4),(B2,B3,A2),(B2,B3,A3),(B2,B3,B4),
(II)其中选出的3人均是工程师选法,共有
| C | 2 3 |
| C | 1 1 |
(B1,B2,B4),(B1,B3,B4),(B2,B3,B4),
故选出的3人均是工程师的概率P=
| 3 |
| 18 |
| 1 |
| 6 |
(III)选出的3人中至少有1名高级工程师和选出的3人均是工程师互为对立事件,
故选出的3人中至少有1名高级工程师的概率P=1-
| 1 |
| 6 |
| 5 |
| 6 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
已知△ABC的内角A、B、C的对边分别为a、b、c,若a2-c2=b2+bc,则A=( )
| A、30° | B、60° |
| C、120° | D、150° |
cos20°sin65°-sin20°cos65°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|

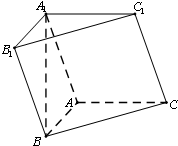 如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.
如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.