题目内容
2.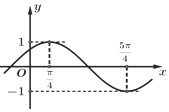 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.(Ⅰ)求f(x)的表达式;
(Ⅱ)把函数y=f(x)的图象向右平移$\frac{π}{4}$个单位后得到函数g(x)的图象,若函数$h(x)=ax+\frac{1}{2}g(2x)-g(x)$在(-∞,+∞)单调递增,求实数a的取值范围.
分析 (Ⅰ)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,可得h(x)的解析式,再根据h′(x)≥0恒成立,求得a的范围.
解答 解:(Ⅰ)根据函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象,
可得A=1,$\frac{T}{2}$=$\frac{5π}{4}$-$\frac{π}{4}$=$\frac{π}{ω}$,∴ω=1.
再根据五点法作图可得1•$\frac{π}{4}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{4}$,∴f(x)=sin(x+$\frac{π}{4}$).
(Ⅱ)把函数y=f(x)的图象向右平移$\frac{π}{4}$个单位后得到函数g(x)=sin(x-$\frac{π}{4}$+$\frac{π}{4}$)=sinx的图象
函数$h(x)=ax+\frac{1}{2}g(2x)-g(x)$=ax+$\frac{1}{2}$sin2x-sinx 在(-∞,+∞)单调递增,
∴h′(x)=a+cos2x-cosx=2cos2x-cosx-1+a=2${(cosx-\frac{1}{4})}^{2}$-$\frac{9}{8}$+a≥0恒成立,
∴-$\frac{9}{8}$+a≥0恒成立,即a≥$\frac{9}{8}$恒成立,故a的范围为[$\frac{9}{8}$,+∞).
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值.还考查了函数y=Asin(ωx+φ)的图象变换规律,利用导数研究函数的单调性,函数的恒成立问题,属于中档题.

| A. | $\left\{\begin{array}{l}{a=-1}\\{b=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=0}\\{b=-1}\end{array}\right.$ |
| A. | 函数f(x)的最大值为$3+\frac{1}{e}$ | B. | 函数f(x)的最小值为$3+\frac{1}{e}$ | ||
| C. | 函数f(x)的最大值为3 | D. | 函数f(x)的最小值为3 |
| 1 | 3 | 5 | 7 | |
| 15 | 13 | 11 | 9 | |
| 17 | 19 | 21 | 23 | |
| 31 | 29 | 27 | 25 | |
| … | … | … | … | … |
南山一棵竹,竹尾风割断,剩下三十节,一节一个圈.头节高五寸①,头圈一尺三②.
逐节多三分③,逐圈少分三④.一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是多远?
此民谣提出的问题的答案是( )
(注:①五寸即0.5尺.②一尺三即1.3尺.③三分即0.03尺.④分三即一分三厘,等于0.013尺.)
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x≥0,x2+x-1<0”的否定是“?x<0,x2+x-1<0” | |
| C. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题. |