题目内容
在n个人的班级中,选出m个人参加大扫除,其中k个人擦窗户,其他人拖地板.现有两种方法选择人选:①先从班级中选出m人,现从他们当中选出k个人擦窗户.②先从班级中选出k个人擦窗户,再从班级剩下的人中选出m-k人拖地板.
(1)写出每种方法中选人方案数的数学表达式.
(2)你认为这两种方法选人的方案数相等吗?若相等,试证明之;若不相等请说明理由.
(1)写出每种方法中选人方案数的数学表达式.
(2)你认为这两种方法选人的方案数相等吗?若相等,试证明之;若不相等请说明理由.
考点:排列、组合的实际应用
专题:计算题,排列组合
分析:(1)根据题意,运用分步计数原理分别求出两种方法的选人方案数即可;
(2)要证明
=
,运用组合数公式可以将左边变形可得左边=
,同理右边也可变形为
,即可证明两种方法选人的方案数相等.
(2)要证明
| C | m n |
| C | k m |
| C | k n |
| C | m-k n-k |
| n! |
| k!×(n-m)!×(m-k)! |
| n! |
| k!×(n-m)!×(m-k)! |
解答:
解(1)对于第一种方法:先从班级中选出m人,有
种方法,再从这m人中选出k个人擦窗户,有
种方法,则第一种方法的选人方案数为
;
对于第二种方法:先从班级中选出k个人擦窗户,有
种方法,再从班级剩下的人中选出m-k人拖地板,有
种方法,则第二种方法选人方案数为
;
故第一种方法的选人方案数为
;第二种方法选人方案数为
;
(2)这两种方法的选人方案数相等,即
=
;
证明如下:
左边=
×
=
;
右边=
×
=
;
左边=右边;
即两种方法选人的方案数相等.
| C | m n |
| C | k m |
| C | m n |
| C | k m |
对于第二种方法:先从班级中选出k个人擦窗户,有
| C | k n |
| C | m-k n-k |
| C | k n |
| C | m-k n-k |
故第一种方法的选人方案数为
| C | m n |
| C | k m |
| C | k n |
| C | m-k n-k |
(2)这两种方法的选人方案数相等,即
| C | m n |
| C | k m |
| C | k n |
| C | m-k n-k |
证明如下:
左边=
| n! |
| m!(n-m)! |
| m! |
| k!(m-k)! |
| n! |
| k!×(n-m)!×(m-k)! |
右边=
| n! |
| k!(n-k)! |
| (n-k)! |
| (m-k)!(n-m)! |
| n! |
| k!×(n-m)!×(m-k)! |
左边=右边;
即两种方法选人的方案数相等.
点评:本题考查组合数的应用,解题的关键是正确理解组合的意义以及运用组合数公式.

练习册系列答案
相关题目
若在△ABC中,有sin
=cosA,则△ABC一定是( )
| C |
| 2 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等腰三角形 |
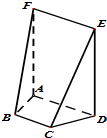 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=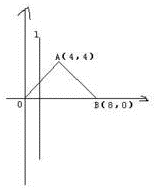 如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB所得图形的面积为S,它与x轴的交点为(x,0).
如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB所得图形的面积为S,它与x轴的交点为(x,0).