题目内容
已知集合A={y|y=x2+2x，-2≤x≤2}，B={x|x2+2x-3≤0}，在集合A中任意取一个元素a，则a∈B的概率是 ．
考点：几何概型
专题：概率与统计
分析：求出集合对应的关系，利用几何概型的概率公式即可得到结论．
解答：
解：A={y|y=x2+2x，-2≤x≤2}={y|-1≤y≤8}，
B={x|x=x2+2x-3≤0}={x|-3≤x≤1}，
若a∈B，则-1≤a≤1
∴由几何概型的概率公式得集合A中任意取一个元素a，则a∈B的概率P=
=
，
故答案为：
B={x|x=x2+2x-3≤0}={x|-3≤x≤1}，
若a∈B，则-1≤a≤1
∴由几何概型的概率公式得集合A中任意取一个元素a，则a∈B的概率P=
| 1-(-1) |
| 8-(-1) |
| 2 |
| 9 |
故答案为：
| 2 |
| 9 |
点评：本题主要考查几何概型的概率计算，利用不等式求出集合对应的元素，结合长度之比是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
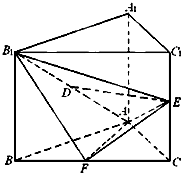已知直三棱柱ABC-A1B1C1中，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1，D、E、F分别为B1A、C1C、BC的中点．