题目内容
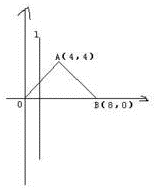 如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB所得图形的面积为S,它与x轴的交点为(x,0).
如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB所得图形的面积为S,它与x轴的交点为(x,0).(1)求函数S=f(x)的解析式;
(2)求函数S=f(x)的定义域、值域;
(3)作函数S=f(x)的图象.
考点:函数解析式的求解及常用方法,函数的图象
专题:函数的性质及应用
分析:(1)根据x的取值情况进行讨论,然后,写成分段函数的形式;
(2)根据(1),借助于函数的单调性求解值域问题;
(3)结合分段函数的特点,按段作出它们的图象.
(2)根据(1),借助于函数的单调性求解值域问题;
(3)结合分段函数的特点,按段作出它们的图象.
解答:
解:(1)当0≤x≤4时,
s=f(x)=
x•x=
x2,
当4<x≤8时,
s=f(x)=S△OAB-
(8-x)2
=
×8×4-
(8-x)2
=16-
(x-8)2,
所以函数的解析式为:
s=f(x)=
.
(2)根据(1),得到函数的定义域为[0,8],
当0≤x≤4时,
s=f(x)=
x•x=
x2,
在[0,4]上为增函数,
所以,s∈[0,8];
当4<x≤8时,
s=f(x)=16-
(x-8)2,
在(4,8]为增函数,
∴s∈(8,16],
综上,函数的值域为[0,16].
(3)函数图象如下图所示:
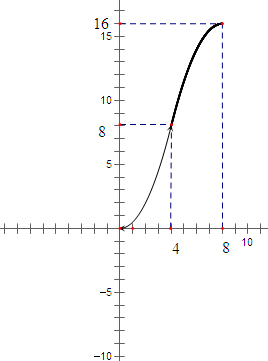
s=f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
当4<x≤8时,
s=f(x)=S△OAB-
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=16-
| 1 |
| 2 |
所以函数的解析式为:
s=f(x)=
|
(2)根据(1),得到函数的定义域为[0,8],
当0≤x≤4时,
s=f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
在[0,4]上为增函数,
所以,s∈[0,8];
当4<x≤8时,
s=f(x)=16-
| 1 |
| 2 |
在(4,8]为增函数,
∴s∈(8,16],
综上,函数的值域为[0,16].
(3)函数图象如下图所示:

点评:本题重点考查分段函数的简单应用,函数的单调性及其运用等知识,属于中档题,考查分类讨论思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
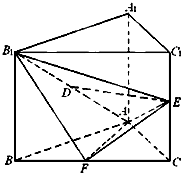 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.