题目内容
已知f(x)是定义在R上的奇函数,当x≥0时f(x)=ex+m(m为常数),则f(-ln5)的值为( )
| A、-4 | B、4 | C、-6 | D、6 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用奇函数的性质f(0)=0可得m,再利用f(x)=-f(-x)即可得出.
解答:
解:∵f(x)是定义在R上的奇函数,当x≥0时,f(x)=ex+m(m为常数),
∴f(0)=e0+m=0,解得m=-1.
∴当x≥0时,f(x)=ex-1,
∴f(ln5)=eln5-1=4.
∴f(-ln5)=-f(ln5)=-4.
故选:A.
∴f(0)=e0+m=0,解得m=-1.
∴当x≥0时,f(x)=ex-1,
∴f(ln5)=eln5-1=4.
∴f(-ln5)=-f(ln5)=-4.
故选:A.
点评:本题考查了奇函数的性质与对数的运算法则,属于基础题.

练习册系列答案
相关题目
如图,当x1=6,x2=9,p=8.5时,x3等于( )
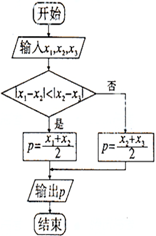

| A、8 | B、4 | C、10 | D、9 |