题目内容
已知两个圆锥有公共底面,且两圆锥的顶点和底面圆周都在半径为3的同一个球面上.若两圆锥的高的比为1:2,则两圆锥的体积之和为 .
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:求出两圆锥的高为2,4,圆锥的底面半径为
=2
,即可求出两圆锥的体积之和.
| 9-1 |
| 2 |
解答:
解:∵两圆锥的高的比为1:2,两圆锥的高的和为6,
∴两圆锥的高为2,4,
∴圆锥的底面半径为
=2
,
∴两圆锥的体积之和为
π•(2
)2•6=16π,
故答案为:16π.
∴两圆锥的高为2,4,
∴圆锥的底面半径为
| 9-1 |
| 2 |
∴两圆锥的体积之和为
| 1 |
| 3 |
| 2 |
故答案为:16π.
点评:本题是中档题,考查旋转体的体积,球的内接圆锥的体积的计算,考查计算能力,空间想象能力,常考题型.

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x≥0时f(x)=ex+m(m为常数),则f(-ln5)的值为( )
| A、-4 | B、4 | C、-6 | D、6 |
函数f(x)=
+lg(x+1)的定义域为( )
| 3x2 | ||
|
| A、(-1,1) |
| B、(-1,+∞) |
| C、(1,+∞) |
| D、(-∞,1) |
函数f(x)=lnx+x2-4零点所在的大致区间为( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
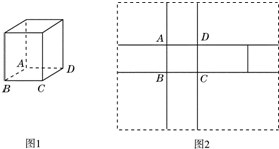 图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是
图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是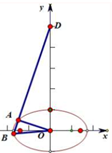 如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.
如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.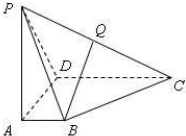 如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=