题目内容
已知函数φ(x)=
,a为常数.
(1)若f(x)=lnx+φ(x),且a=
,求函数f(x)的单调区间;
(2)若g(x)=|lnx|+φ(x),且对任意x1,x2∈(0,2],当x1≠x2时,都有
<-1,求a的取值范围.
| a |
| x+1 |
(1)若f(x)=lnx+φ(x),且a=
| 9 |
| 2 |
(2)若g(x)=|lnx|+φ(x),且对任意x1,x2∈(0,2],当x1≠x2时,都有
| g(x2)-g(x1) |
| x 2-x 1 |
考点:利用导数求闭区间上函数的最值,对数函数图象与性质的综合应用
专题:综合题,分类讨论,函数思想,导数的综合应用
分析:(1)对f(x)求导,利用f′(x)>0判断函数单调增,f′(x)<0函数单调减,求出单调区间;
(2)由题意,构造函数h(x)=g(x)+x,根据h(x)在(0,2]上的单调性,再利用导数讨论h(x)的单调性与最值问题,从而求出a的取值范围.
(2)由题意,构造函数h(x)=g(x)+x,根据h(x)在(0,2]上的单调性,再利用导数讨论h(x)的单调性与最值问题,从而求出a的取值范围.
解答:
解:(1)∵f(x)=lnx+φ(x)=lnx+
,(x>0);
∴f′(x)=
-
=
,
当a=
时,令f′(x)>0,即x2-
x+1>0,
解得x>2,或x<
,
∴函数f(x)的单调增区间为(0,
),(2,+∞),单调减区间为(
,2);---5分(注:两个单调增区间,错一个扣1分)
(2)∵
<-1,∴
+1<0,
即
<0;
设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数;---8分
当1≤x≤2时,h(x)=lnx+
+x,h′(x)=
-
+1;
令h′(x)≤0,解得a≥
+(x+1)2=x2+3x+
+3对x∈[1,2]时恒成立;
设m(x)=x2+3x+
+3,则m′(x)=2x+3-
,
∵1≤x≤2,∴m′(x)=2x+3-
>0,
∴m(x)在[1,2]上是增函数,则当x=2时,m(x)的最大值为
,∴a≥
;…11分
当0<x<1时,h(x)=-lnx+
+x,h′(x)=-
-
+1,
令h′(x)≤0,解得a≥-
+(x+1)2=x2+x-
-1,
设t(x)=x2+x-
-1,则t′(x)=2x+1+
>0,
∴t(x)在(0,1)上是增函数,∴t(x)<t(1)=0,∴a≥0;---13分
综上所述,a的取值范围{a|a≥
}.---14分
| a |
| x+1 |
∴f′(x)=
| 1 |
| x |
| a |
| (x+1)2 |
| x2+(2-a)x+1 |
| x(x+1)2 |
当a=
| 9 |
| 2 |
| 5 |
| 2 |
解得x>2,或x<
| 1 |
| 2 |
∴函数f(x)的单调增区间为(0,
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵
| g(x2)-g(x1) |
| x2-x1 |
| g(x2)-g(x1) |
| x2-x1 |
即
| g(x2)+x2-[g(x1)+x1] |
| x2-x1 |
设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数;---8分
当1≤x≤2时,h(x)=lnx+
| a |
| x+1 |
| 1 |
| x |
| a |
| (x+1)2 |
令h′(x)≤0,解得a≥
| (x+1)2 |
| x |
| 1 |
| x |
设m(x)=x2+3x+
| 1 |
| x |
| 1 |
| x2 |
∵1≤x≤2,∴m′(x)=2x+3-
| 1 |
| x2 |
∴m(x)在[1,2]上是增函数,则当x=2时,m(x)的最大值为
| 27 |
| 2 |
| 27 |
| 2 |
当0<x<1时,h(x)=-lnx+
| a |
| x+1 |
| 1 |
| x |
| a |
| (x+1)2 |
令h′(x)≤0,解得a≥-
| (x+1)2 |
| x |
| 1 |
| x |
设t(x)=x2+x-
| 1 |
| x |
| 1 |
| x2 |
∴t(x)在(0,1)上是增函数,∴t(x)<t(1)=0,∴a≥0;---13分
综上所述,a的取值范围{a|a≥
| 27 |
| 2 |
点评:本题考查了导数的综合应用问题,也考查了构造函数来研究函数的单调性与最值问题和分类讨论思想,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设数列{an}是公差d<0的等差数列,Sn为其前n项和,若S6=5a1+10d,则Sn取最大值时,n=( )
| A、5 | B、6 | C、5或6 | D、6或7 |
已知f(x)是定义在R上的奇函数,当x≥0时f(x)=ex+m(m为常数),则f(-ln5)的值为( )
| A、-4 | B、4 | C、-6 | D、6 |
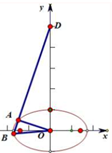 如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.
如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.