题目内容
某单位拟安排6名职工在春节放假期间(正月初一、初二、初三)值班,每天安排2人,每人值班1天,若6位职工中的甲不值正月初一,乙不值正月初三,则不同的安排方法共有 种.
考点:排列、组合的实际应用
专题:计算题,概率与统计
分析:用间接法分析,首先计算计算6名职工在3天值班的所有情况数目,再排除其中甲在正月初一和乙在正月初三值班的情况数目,再加上甲在正月初一且乙在正月初三值班的数目,即可得答案.
解答:
解:根据题意,先安排6人在3天值班,有C62×C42×C22种情况,
其中甲在正月初一值班有C51×C42×C22种情况,
乙在正月初三值班有C51×C42×C22种情况,
甲在正月初一且乙在正月初三值班有C41×C31种情况,
则不同的安排方法共有C62×C42×C22-2×C51×C42×C22+C41×C31=42种,
故答案为42.
其中甲在正月初一值班有C51×C42×C22种情况,
乙在正月初三值班有C51×C42×C22种情况,
甲在正月初一且乙在正月初三值班有C41×C31种情况,
则不同的安排方法共有C62×C42×C22-2×C51×C42×C22+C41×C31=42种,
故答案为42.
点评:本题考查排列、组合的运用,注意用间接法进行分析,必须分析其中是否有重复或遗漏的情况.

练习册系列答案
相关题目
平面向量
=(-1,1),
=(1,2),且
•
=3,则
•
=( )
| AB |
| n |
| n |
| AC |
| n |
| BC |
| A、-2 | B、2 | C、3 | D、4 |
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )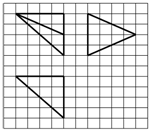

A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(1,-1),
=(2,m),若
⊥
,则m=( )
| a |
| b |
| a |
| b |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
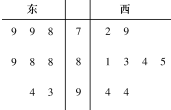 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.