题目内容

如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为（　　）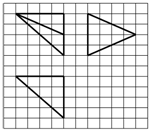
A、
32
3
B、
16
3
C、
64
3
D、
8
3
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图，得出该几何体是棱长为4的正方体内的三棱锥，求出体积即可．
解答： 解：根据几何体的三视图得，
该几何体是如图所示的棱长为4的正方体内的三棱锥E-CC1D1（其中E为BB1的中点），

该几何体的体积是
V锥E-CC1D1=
1
3
Sh=
1
3
×（
1
2
×4×4）×4=
32
3
．
故选：A．
点评：本题考查了空间几何体的三视图的应用问题，解题时应根据三视图得出几何体是什么图形，是基础题．
练习册系列答案
相关题目
已知命题p：m2-m＜0，命题q：
y2
2
+
x2
1+4m2
=1表示焦点在y轴上的椭圆．
（Ⅰ）若p∧q是真命题，求实数m的取值范围；
（Ⅱ） 若椭圆
y2
2
+
x2
1+4m2
=1的焦点到双曲线
x2
2
-
y2
2
=1的渐近线的距离为
2
2
，求m的值．
平面向量
a
，
b
，
e
满足：|
e
|=1，
a
•
e
=1，
b
•
e
=2，|
a
-
b
|=2，则向量
a
-
b
与
e
的夹角为
 
．
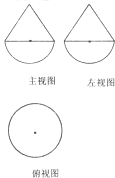已知一个几何体是由上、下两部分构成的组合体，其三视图如图，若图中圆的半径为l，等腰三角形的腰长为
5
；，则该几何体的表面积是
 
．
已知函数f（x）=（2
3
cosx+sinx）sinx-sin2（
π
2
+x）．
（Ⅰ）求函数f（x）的单调减区间；
（Ⅱ）△ABC的内角A、B、C的对边分别为a，b，c，已知f（
C
2
）=2，c=2，且sinB=3sinA，求△ABC的面积．
某单位拟安排6名职工在春节放假期间（正月初一、初二、初三）值班，每天安排2人，每人值班1天，若6位职工中的甲不值正月初一，乙不值正月初三，则不同的安排方法共有
 
种．
已知定义在R上的奇函数f（x）满足f（x+2）=-f（x），则f（4）的值是（　　）
A、-1B、0C、1D、2
若函数f（x）=
ax+b
x2+1
是偶函数，且f（1）=2．
（1）求a、b的值及f（x）；
（2）判断函数f（x）在区间（0，+∞）上的单调性，并证明你的结论．
tan300°=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网