题目内容

已知向量
a
=（1，-1），
b
=（2，m），若
a
⊥
b
，则m=（　　）
A、-2
B、-
1
2
C、
1
2
D、2
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：
a
⊥
b
?
a
•
b
=0，利用向量数量积的坐标运算得出关于m的方程求解即可．
解答： 解：
a
=（1，-1），
b
=（2，m）
a
⊥
b
，则
a
•
b
=0，即2×1+（-1）m=0，解得m=2
故选：D．
点评：本题考查了向量数量积的坐标运算，是简答题
练习册系列答案
相关题目
某单位拟安排6名职工在春节放假期间（正月初一、初二、初三）值班，每天安排2人，每人值班1天，若6位职工中的甲不值正月初一，乙不值正月初三，则不同的安排方法共有
 
种．
如图，直线x=±π，y=±1围成的矩形区域内有一段余弦曲线y=-cosx，任意地向矩形投掷飞镖，则飞镖落入阴影区域的概率是
 
．
函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|≤
π
6
，x∈R）的部分图象如图所示，则该函数表达式为（　　）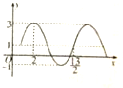
A、y=2sin（
π
3
x-
π
6
）+1
B、y=2sin（
π
6
x-
π
3
）
C、y=2sin（
π
3
x+
π
6
）+1
D、y=2sin（
π
6
x+
π
3
）+1
tan300°=
 
．
等比数列{an}中，a4=4，则a2•a6等于（　　）
A、4B、8C、16D、32
若函数y=loga（ax2+3ax+2）的值域为R，则a的取值范围是
 
．
函数y=
1-lnx
的定义域为（　　）
A、（0，e]
B、（-∞，e]
C、（0，10]
D、（-∞，10]
函数y=
2-x
lg(2x-2)
的定义域为（　　）
A、[1，2]
B、（1，2]
C、(1，
3
2
)∪(
3
2
，2]
D、[1，
3
2
)∪(
3
2
，2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网