题目内容
某种商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系式近似满足P=
,商品的日销售量Q(件)与时间t(天)的函数关系式近似满足Q=-t+40(1≤t≤30,t∈N).
(1)求这种商品日销售金额y与时间t的函数关系式;
(2)求y的最大值,并指出日销售金额最大的一天是30天中第几天.
|
(1)求这种商品日销售金额y与时间t的函数关系式;
(2)求y的最大值,并指出日销售金额最大的一天是30天中第几天.
考点:函数的最值及其几何意义
专题:计算题,应用题,函数的性质及应用
分析:(1)设日销售金额为y元,则y=P•Q,利用分段函数写出函数表达式;
(2)当1≤t≤24时,y=-(t-10)2+900,当25≤t≤30时,y=(t-70)2-900,分别求最值,从而得到分段函数的最值及最值点.
(2)当1≤t≤24时,y=-(t-10)2+900,当25≤t≤30时,y=(t-70)2-900,分别求最值,从而得到分段函数的最值及最值点.
解答:
解:(1)设日销售金额为y元,则y=P•Q,
即,y=
,t∈N;
(2)当1≤t≤24时,y=-(t-10)2+900,
故当t=10时,ymax=900;
当25≤t≤30时,y=(t-70)2-900,
故当t=25时,ymax=1125.
故该商品日销售金额的最大值为1125元,且近30天中第25天销售金额最大.
即,y=
|
(2)当1≤t≤24时,y=-(t-10)2+900,
故当t=10时,ymax=900;
当25≤t≤30时,y=(t-70)2-900,
故当t=25时,ymax=1125.
故该商品日销售金额的最大值为1125元,且近30天中第25天销售金额最大.
点评:本题考查了学生将实际问题转化为数学问题的能力,同时考查了分段函数的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)满足f(x+1)=
,且当x∈(0,1]时,f(x)=x,g(x)=m(x+3),若方程f(x)=g(x)在区间(-1,1]上有两个不同的实根,则实数m的取值范围是( )
| 1 |
| f(x)+1 |
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则f(4)的值是( )
| A、-1 | B、0 | C、1 | D、2 |
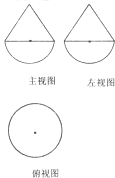 已知一个几何体是由上、下两部分构成的组合体,其三视图如图,若图中圆的半径为l,等腰三角形的腰长为
已知一个几何体是由上、下两部分构成的组合体,其三视图如图,若图中圆的半径为l,等腰三角形的腰长为 如图,直线x=±π,y=±1围成的矩形区域内有一段余弦曲线y=-cosx,任意地向矩形投掷飞镖,则飞镖落入阴影区域的概率是
如图,直线x=±π,y=±1围成的矩形区域内有一段余弦曲线y=-cosx,任意地向矩形投掷飞镖,则飞镖落入阴影区域的概率是