题目内容
设函数f(x)=x2+c,g(x)=aex的图象的一个公共点为(2,t),且曲线y=f(x),y=g(x)在P点处有相同切线,函数f(x)-g(x)的负零点在区间(k,2k+1),k∈Z,则k= .
考点:利用导数研究曲线上某点切线方程,函数零点的判定定理
专题:导数的综合应用
分析:由题意知f′(2)=g′(2),即4=ae2①,f(2)=g(2),即4+c=ae2②,联立①②可求a,c,从而得f(x)-g(x),利用导数可判断函数在(-∞,0)上的单调性,由零点判定定理可知零点的存在的区间,由此可求k.
解答:
解:f′(x)=2x,g′(x)=aex,
∵曲线y=f(x),y=g(x)在P(2,t)点处有相同的切线,
∴f′(2)=g′(2),即4=ae2,①
又P为两曲线的公共点,
∴f(2)=g(2),即4+c=ae2,②
由①②解得c=0,a=
,
令h(x)=f(x)-g(x)=x2-
•ex=x2-4ex-2,
则h′(x)=2x-4ex-2,
当x≤0时,h′(x)<0,∴h(x)在(-∞,0)上递减,
又h(-1)=1-4e-3>0,h(0)=-4e-2<0,
∴h(x)在(-1,0)内有唯一零点,
由题意知(k,k+1)=(-1,0),
∴k=-1.
故答案为:-1.
∵曲线y=f(x),y=g(x)在P(2,t)点处有相同的切线,
∴f′(2)=g′(2),即4=ae2,①
又P为两曲线的公共点,
∴f(2)=g(2),即4+c=ae2,②
由①②解得c=0,a=
| 4 |
| e2 |
令h(x)=f(x)-g(x)=x2-
| 4 |
| e2 |
则h′(x)=2x-4ex-2,
当x≤0时,h′(x)<0,∴h(x)在(-∞,0)上递减,
又h(-1)=1-4e-3>0,h(0)=-4e-2<0,
∴h(x)在(-1,0)内有唯一零点,
由题意知(k,k+1)=(-1,0),
∴k=-1.
故答案为:-1.
点评:本题考查利用导数研究曲线上某点的切线方程,考查函数的零点判定定理.曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知数列{an}是等差数列,满足a2=5,a4=13.数列{bn}的前n项和是Tn,且Tn+bn=3.
(1)求数列{an}及数列{bn}的通项公式;
(2)若cn=an•bn,求数列{cn}中的最大项.
(1)求数列{an}及数列{bn}的通项公式;
(2)若cn=an•bn,求数列{cn}中的最大项.
已知x,y满足不等式组
,则Z=x+2y的最小值为( )
|
| A、2 | B、3 | C、4 | D、-6 |
下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,则能得出AB∥平面MNP的图形个数是( )
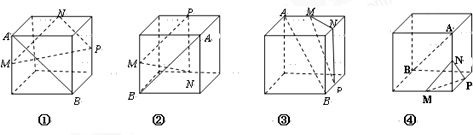

| A、1个 | B、2个 | C、3个 | D、4个 |
 在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为
在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为