题目内容
函数y=
的定义域为(0,
],则a= .
| 2logax-3 |
| 1 |
| 27 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:要使f(x)有意义,则2logaX-3≥0,故logax≥
,
由于x的解符合(0,
],可得0<a<1,且(a)
=
,可求出a.
| 3 |
| 2 |
由于x的解符合(0,
| 1 |
| 27 |
| 3 |
| 2 |
| 1 |
| 27 |
解答:
解:要使f(x)有意义,则2logaX-3≥0,
∴logax≥
,
由于x的解符合(0,
],∴0<a<1
∴logax≥
得0<x≤(a)
,∴(a)
=
,
∴a=
故答案为
∴logax≥
| 3 |
| 2 |
由于x的解符合(0,
| 1 |
| 27 |
∴logax≥
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 27 |
∴a=
| 1 |
| 9 |
故答案为
| 1 |
| 9 |
点评:本题考查:函数的定义域、函数的值域,要熟记指数、对数函数的有关性质,本题属于基础题.

练习册系列答案
相关题目
等比数列{an}中a2=4,a5=32则{an}的前6项和为( )
| A、128 | B、126 |
| C、140 | D、192 |
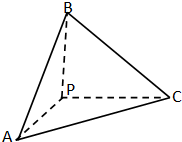 三棱锥P-ABC中,三侧棱PA,PB,PC两两互相垂直,且三角形△PAB,△PAC,△PBC的面积依次为1,1,2,则此三棱锥 P-ABC外接球的表面积为( )
三棱锥P-ABC中,三侧棱PA,PB,PC两两互相垂直,且三角形△PAB,△PAC,△PBC的面积依次为1,1,2,则此三棱锥 P-ABC外接球的表面积为( )| A、9π | B、12π |
| C、18π | D、36π |
下列函数中,不是奇函数的为( )
A、y=ln
| ||
| B、y=-x3 | ||
| C、y=ex+e-x | ||
| D、y=x|x| |
若0<α<
,则经过两点P1(0,cosα),P2(sinα,0)的直线的倾斜角为( )
| π |
| 2 |
| A、α$ | ||
B、
| ||
| C、π-α | ||
| D、-α |
设a=ln2,b=(ln2)2,c=ln
,则( )
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、c>b>a |