题目内容
如果实数x,y满足等式y2=x,那么
的最大值是( )
| y |
| x+1 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,
=
,分类讨论,利用基本不等式,即可求出
的最大值.
| y |
| x+1 |
| y |
| y2+1 |
| y |
| x+1 |
解答:
解:由题意,
=
,
y=0时,
=0,
y≠0时,|
|=|
|=|
|≤
,
∴
的最大值是
,
故选:D.
| y |
| x+1 |
| y |
| y2+1 |
y=0时,
| y |
| x+1 |
y≠0时,|
| y |
| x+1 |
| y |
| y2+1 |
| 1 | ||
y+
|
| 1 |
| 2 |
∴
| y |
| x+1 |
| 1 |
| 2 |
故选:D.
点评:本题考查抛物线的性质,考查基本不等式的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
在△ABC中,三边a,b,c所对的角分别为A,B,C,若a2-b2=
bc,sinC=2
sinB,则角A=( )
| 3 |
| 3 |
| A、30° | B、45° |
| C、150° | D、135° |
从2名男生和2名女生中,任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若满足条件
的点P(x,y)构成三角形区域,则实数k的取值范围是( )
|
| A、(1,+∞) |
| B、(0,1) |
| C、(-1,1) |
| D、(-∞,-1)∪(1,+∞) |
设函数f(x)的导函数为f′(x),若对任意x∈R都有f′(x)>f(x)成立,则( )
| A、f(ln2014)<2014f(0) |
| B、f(ln2014)=2014f(0) |
| C、f(ln2014)>2014f(0) |
| D、f(ln2014)与2014f(0)的大小关系不确定 |
设|
|=2,|
|=3,∠BAC=60°,
=2
,
=x
+(1+x)
,x∈[0,1],则
在
上的投影的取值范围是( )
| AB |
| AC |
| CD |
| BC |
| AE |
| AD |
| AB |
| AE |
| AC |
| A、[0,1] |
| B、[0,7] |
| C、[1,9] |
| D、[9,21] |
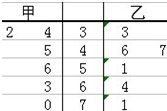 近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.其形成与PM2.5有关.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见表:
近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.其形成与PM2.5有关.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见表: