题目内容
设函数f（x）的导函数为f′（x），若对任意x∈R都有f′（x）＞f（x）成立，则（ ）
| A、f（ln2014）＜2014f（0） |
| B、f（ln2014）=2014f（0） |
| C、f（ln2014）＞2014f（0） |
| D、f（ln2014）与2014f（0）的大小关系不确定 |
考点：导数的运算
专题：函数的性质及应用
分析：构造函数g（x）=
，利用导数可判断g（x）的单调性，由单调性可得g（ln2014）与g（0）的大小关系，整理即可得到答案．
| f(x) |
| ex |
解答：
令g（x）=
，则g′（x）=
=
，
因为对任意x∈R都有f′（x）＞f（x），
所以g′（x）＞0，即g（x）在R上单调递增，
又ln2014＞0，所以g（ln2014）＞g（0），即
＞
，
所以 f（ln2014）＞2014f（0），
故选：C．
| f(x) |
| ex |
| f′(x)•ex-f(x)•e x |
| e2x |
| f′(x)-f(x) |
| ex |
因为对任意x∈R都有f′（x）＞f（x），
所以g′（x）＞0，即g（x）在R上单调递增，
又ln2014＞0，所以g（ln2014）＞g（0），即
| f(ln2014) |
| eln2014 |
| f(0) |
| e0 |
所以 f（ln2014）＞2014f（0），
故选：C．
点评：本题考查导数的运算及利用导数研究函数的单调性，属中档题，解决本题的关键是根据选项及已知条件合理构造函数，利用导数判断函数的单调性．
练习册系列答案
走进文言文系列答案
相关题目
抛物线y2=4x上一点P到直线x=-1的距离与到点Q（2，2）的距离之差的最大值为（ ）
| A、3 | ||
B、
| ||
| C、5 | ||
D、
|
如果实数x，y满足等式y2=x，那么
的最大值是（ ）
| y |
| x+1 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
设双曲线
-
=1（a＞0）的渐近线方程为3x±2y=0，则
（
）dx的值为（ ）
| x2 |
| a2 |
| y2 |
| 9 |
| ∫ | a 1 |
| 1 |
| x |
| A、ln2 | B、0 | C、ln3 | D、1 |
若平面向量
，
的夹角为60°，且|
|=2|
|，则（ ）
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
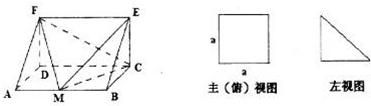
一个多面体的直观图和三视图所示，M是AB的中点，一只蝴蝶在几何体ADF-BCE内自由飞翔，由它飞入几何体F-AMCD内的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|