题目内容
为了考察某校各班参加数学竞赛的人数,在全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为7,样本方差为4,且样本数据互相不相同,则样本数据中的最小值为 .
考点:极差、方差与标准差
专题:概率与统计
分析:设样本数据为:x1,x2,x3,x4,x5,由已知条件推导出x1+x2+x3+x4+x5=35,(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2+(x5-7)2=20,由此能求出样本数据中的最小值为4.
解答:
解:设样本数据为:x1,x2,x3,x4,x5,
平均数=(x1+x2+x3+x4+x5)÷5=7;
方差s2=[(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2+(x5-7)2]÷5=4.
从而有x1+x2+x3+x4+x5=35,①
(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2+(x5-7)2=20.②
若样本数据中的最大值为11,不妨设x5=11,则②式变为:
(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2=4,
由于样本数据互不相同,这是不可能成立的.
若样本数据为4,6,7,8,10,
代入验证知①②式均成立,
此时样本数据中的最小值为4.
故答案为:4.
平均数=(x1+x2+x3+x4+x5)÷5=7;
方差s2=[(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2+(x5-7)2]÷5=4.
从而有x1+x2+x3+x4+x5=35,①
(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2+(x5-7)2=20.②
若样本数据中的最大值为11,不妨设x5=11,则②式变为:
(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2=4,
由于样本数据互不相同,这是不可能成立的.
若样本数据为4,6,7,8,10,
代入验证知①②式均成立,
此时样本数据中的最小值为4.
故答案为:4.
点评:本题考查样本数据中的最小值的求法,是中档题,解题时要认真审题,注意平均数公式和方差公式的合理运用.

练习册系列答案
相关题目
执行如图的程序框图,那么输出S的值是( )


| A、2 | ||
B、
| ||
| C、-1 | ||
| D、1 |
抛物线y2=4x上一点P到直线x=-1的距离与到点Q(2,2)的距离之差的最大值为( )
| A、3 | ||
B、
| ||
| C、5 | ||
D、
|
如果实数x,y满足等式y2=x,那么
的最大值是( )
| y |
| x+1 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
一个多面体的直观图和三视图所示,M是AB的中点,一只蝴蝶在几何体ADF-BCE内自由飞翔,由它飞入几何体F-AMCD内的概率为( )
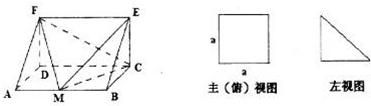

A、
| ||
B、
| ||
C、
| ||
D、
|
