题目内容
设|
|=2,|
|=3,∠BAC=60°,
=2
,
=x
+(1+x)
,x∈[0,1],则
在
上的投影的取值范围是( )
| AB |
| AC |
| CD |
| BC |
| AE |
| AD |
| AB |
| AE |
| AC |
| A、[0,1] |
| B、[0,7] |
| C、[1,9] |
| D、[9,21] |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由向量加法的三角形法则把向量
用向量
,
表示,代入
=x
+(1+x)
,然后求出
•
,
再由
•
=|
|•|
|cos<
,
>,两边同时乘以
得到
在
上的投影关于x的函数,最后由x的范围求得答案.
| AD |
| AB |
| AC |
| AE |
| AD |
| AB |
| AE |
| AC |
再由
| AE |
| AC |
| AE |
| AC |
| AE |
| AC |
| 1 | ||
|
|
| AE |
| AC |
解答:
解:∵
=2
,
∴
=
+
=
+2
,
=
+2
-2
=3
-2
,
∴
=x
+(1+x)
=x(3
-2
)+(1+x)
=3x
+(1-x)
.
又|
|=2,|
|=3,∠BAC=60°,
则
•
=[3x
+(1-x)
]•
=3x•|
|2+(1-x)•|
|•|
|•cos60°
=27x+(1-x)•2•3•
=24x+3.
由
•
=|
|•|
|cos<
,
>,
∴|
|cos<
,
>=
=
=8x+1.
∵x∈[0,1],
∴8x+1∈[1,9].
∴
在
上的投影的取值范围是[1,9].
故选:C.
| CD |
| BC |
∴
| AD |
| AC |
| CD |
| AC |
| BC |
=
| AC |
| AC |
| AB |
| AC |
| AB |
∴
| AE |
| AD |
| AB |
=x(3
| AC |
| AB |
| AB |
| AC |
| AB |
又|
| AB |
| AC |
则
| AE |
| AC |
| AC |
| AB |
| AC |
=3x•|
| AC |
| AB |
| AC |
=27x+(1-x)•2•3•
| 1 |
| 2 |
由
| AE |
| AC |
| AE |
| AC |
| AE |
| AC |
∴|
| AE |
| AE |
| AC |
| ||||
|
|
| 24x+3 |
| 3 |
∵x∈[0,1],
∴8x+1∈[1,9].
∴
| AE |
| AC |
故选:C.
点评:本题考查平面向量的数量积运算,考查了向量加法的三角形法则,解答的关键是明确向量在向量上的投影概念,是中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
如果实数x,y满足等式y2=x,那么
的最大值是( )
| y |
| x+1 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
若平面向量
,
的夹角为60°,且|
|=2|
|,则( )
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列说法正确的是( )
| A、命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | ||
B、a∈R,“
| ||
| C、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | ||
D、命题p:“?x∈R,sinx+cosx≤
|
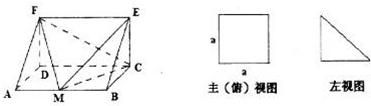
一个多面体的直观图和三视图所示,M是AB的中点,一只蝴蝶在几何体ADF-BCE内自由飞翔,由它飞入几何体F-AMCD内的概率为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
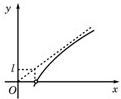
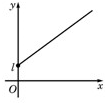

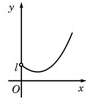
 如图,f(x)=Asin(2ωx+φ)(ω>0,A>0,-π<φ<0).
如图,f(x)=Asin(2ωx+φ)(ω>0,A>0,-π<φ<0).