题目内容
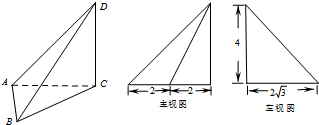
三棱锥D-ABC及其三视图中的主视图和下视图如图所示,则棱BD的长为 .三棱锥D-ABC的体积为 .

考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由主视图知CD⊥平面ABC、B点在AC上的射影为AC中点及AC长,由左视图可知CD长及△ABC中变AC的高,利用勾股定理即可求出棱BD的长;利用棱锥的体积公式,即可得出结论.
解答:
解:由主视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=2;
由左视图知CD=4,BE=2
,
在Rt△BCE中,BC=4,在Rt△BCD中,BD=
=4
.
三棱锥D-ABC的体积为
×
×4×2
×4=
.
故答案为:4
,
由左视图知CD=4,BE=2
| 3 |
在Rt△BCE中,BC=4,在Rt△BCD中,BD=
| 42+42 |
| 2 |
三棱锥D-ABC的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
16
| ||
| 3 |
故答案为:4
| 2 |
16
| ||
| 3 |
点评:本题考查点、线、面间的距离计算,考查空间图形的三视图,考查学生的空间想象能力,考查学生分析解决问题的能力.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
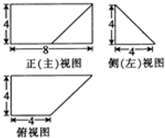
已知某几何体的三视图如图所示,则该几何体的体积等于( )

A、
| ||
| B、160 | ||
C、64+32
| ||
| D、60 |
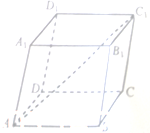
在平行六面体ABCD-A1B1C1D1中,
=x
+2y
+3z
,则x+y+z=( )
| AC1 |
| AB |
| AD |
| AA1 |

A、
| ||
B、
| ||
C、
| ||
D、
|
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
的切线,切点为E,延长FE交双曲线右支于点P,若E为线段PF的中点,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
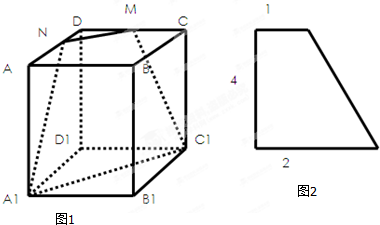
如图1所示,长方体AC1沿截面A1C1MN截得几何体DMN-D1A1C1,它的正视图、侧视图均为图2所示的直角梯形,则该几何体的体积为( )

A、
| ||
B、
| ||
| C、14 | ||
| D、10 |
 我校同学设计了一个如图所示的“蝴蝶形图案”(阴影区域)来庆祝数学学科节目的成功举办,其中AC,BD是过抛物线C的焦点F的两条弦,且F(0,1),
我校同学设计了一个如图所示的“蝴蝶形图案”(阴影区域)来庆祝数学学科节目的成功举办,其中AC,BD是过抛物线C的焦点F的两条弦,且F(0,1),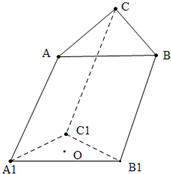 在三棱柱ABC-A1B1C1中,底面△ABC为正三角形且边长为
在三棱柱ABC-A1B1C1中,底面△ABC为正三角形且边长为
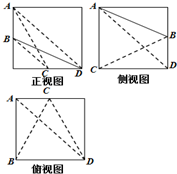 在棱长为2的正方体内有一四面体A-BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A-BCD的体积为( )
在棱长为2的正方体内有一四面体A-BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A-BCD的体积为( )