题目内容
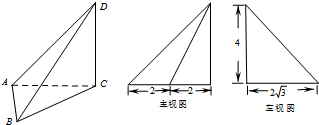
已知某几何体的三视图如图所示,则该几何体的体积等于( )

A、
| ||
| B、160 | ||
C、64+32
| ||
| D、60 |
考点:由三视图求面积、体积
专题:综合题,空间位置关系与距离
分析:由已知中的三视图,我们可以判断该几何体是由一个直三棱柱和一个四棱锥组成,三棱柱的底面是一个直角边长为4的直角三角形,高为4,四棱锥的底面是一个以4为边长的正方形,高为4,分别求出棱柱和棱锥的体积,即可得出结论.
解答:
解:由已知中的三视图,我们可以判断该几何体是由一个直三棱柱和一个四棱锥组成,三棱柱的底面是一个直角边长为4的直角三角形,高为4,四棱锥的底面是一个以4为边长的正方形,高为4,分别求出棱柱和棱锥的体积,其中直三棱的底面为左视图,高为8-4=4,故V直三棱柱=8×4=32,四棱锥的底面为边长为4的正方形,高为4,
故V四棱锥=
×16×4=
,故该几何体的体积V=V直三棱柱+V四棱锥=
,
故选A.
故V四棱锥=
| 1 |
| 3 |
| 64 |
| 3 |
| 160 |
| 3 |
故选A.
点评:由已知中的三视图,判断该几何体是一个直三棱柱和一个四棱锥的组合体是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
某空间几何体的三视图如图所示,则该几何体的体积是( )


| A、4 | B、5 | C、6 | D、7 |
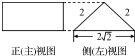 如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8
如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8| 2 |
A、2 0+8
| ||
B、2 4+8
| ||
| C、8 | ||
| D、16 |
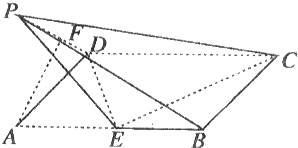
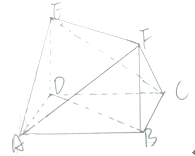 如图,多面体ABCDEF中,底面ABCD是菱形,∠BCD=60°,四边形BDEF是正方形且DE⊥平面ABCD.
如图,多面体ABCDEF中,底面ABCD是菱形,∠BCD=60°,四边形BDEF是正方形且DE⊥平面ABCD.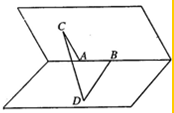 如图,60°的二面角的棱上有A,B两点,线段AC,BD分别在这个二面角的两个半平面内,且AC⊥AB,BD⊥AB,已知AB=4,AC=6,BD=8.
如图,60°的二面角的棱上有A,B两点,线段AC,BD分别在这个二面角的两个半平面内,且AC⊥AB,BD⊥AB,已知AB=4,AC=6,BD=8.