题目内容
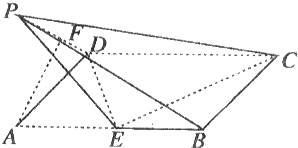
 我校同学设计了一个如图所示的“蝴蝶形图案”(阴影区域)来庆祝数学学科节目的成功举办,其中AC,BD是过抛物线C的焦点F的两条弦,且F(0,1),
我校同学设计了一个如图所示的“蝴蝶形图案”(阴影区域)来庆祝数学学科节目的成功举办,其中AC,BD是过抛物线C的焦点F的两条弦,且F(0,1),| AC |
| BD |
(1)求抛物线的方程;
(2)当“蝴蝶形图案”的面积最小时,求a的大小.
考点:抛物线的简单性质,平面向量数量积的运算
专题:圆锥曲线中的最值与范围问题
分析:(1)由抛物线的焦点坐标即可得到抛物线的标准方程;
(2)由题意结合图形,把A、B、C、D四点的坐标分别用|AF|、|BF|、|CF|、|DF|和α表示,代入抛物线方程后最终求得|AF|、|BF|、|CF|、|DF|,对三角形面积化简整理,换元后利用配方法求面积的最小值.
(2)由题意结合图形,把A、B、C、D四点的坐标分别用|AF|、|BF|、|CF|、|DF|和α表示,代入抛物线方程后最终求得|AF|、|BF|、|CF|、|DF|,对三角形面积化简整理,换元后利用配方法求面积的最小值.
解答:
解:(1)由题意可得抛物线方程为:x2=4y.
(2)解:①由抛物线Γ焦点F(0,1)得,抛物线Γ方程为x2=4y;
②设AF=m,则点A(-msinα,mcosα+1),
∴(-msinα)2=4(1+mcosα),即m2sin2α-4mcosα-4=0.
解得:m=
,
∵m>0,∴|AF|=
.
同理:|BF|=
,|DF|=
,|CF|=
..
“蝴蝶形图案”的面积S=S△AFB+S△CFD=
,令t=sinαcosα,t∈(0,
],
∈[2,+∞).
则S=4•
=4(
-
)2-1,
∴当
=2时,即α=
时“蝴蝶形图案”的面积最小为8.
(2)解:①由抛物线Γ焦点F(0,1)得,抛物线Γ方程为x2=4y;
②设AF=m,则点A(-msinα,mcosα+1),
∴(-msinα)2=4(1+mcosα),即m2sin2α-4mcosα-4=0.

解得:m=
| 2(cosα±1) |
| sin2α |
∵m>0,∴|AF|=
| 2(cosα+1) |
| sin2α |
同理:|BF|=
| 2(1-sinα) |
| cos2α |
| 2(1+sinα) |
| cos2α |
| 2(1-cosα) |
| sin2α |
“蝴蝶形图案”的面积S=S△AFB+S△CFD=
| 4-4sinαcosα |
| (sinαcosα)2 |
| 1 |
| 2 |
| 1 |
| t |
则S=4•
| 1-t |
| t2 |
| 1 |
| t |
| 1 |
| 2 |
∴当
| 1 |
| t |
| π |
| 4 |
点评:本题考查了抛物线的标准方程及其性质、点直线与抛物线的关系、三角函数化简、换元法、二次函数的单调性、向量垂直与数量积的关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
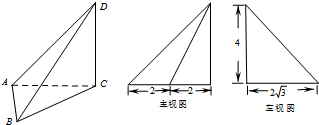
某空间几何体的三视图如图所示,则该几何体的体积是( )


| A、4 | B、5 | C、6 | D、7 |
已知等比数列{an}的前n项和为Sn,则下列选项中一定成立的是( )
| A、若a1>0,则a2015<0 |
| B、若a2>0,则a2016<0 |
| C、若a1>0,则S2015>0 |
| D、若a2>0,则S2016>0 |