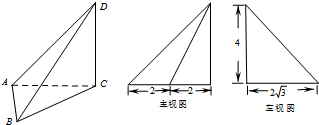
题目内容
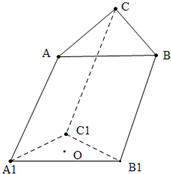 在三棱柱ABC-A1B1C1中,底面△ABC为正三角形且边长为
在三棱柱ABC-A1B1C1中,底面△ABC为正三角形且边长为| 3 |
(Ⅰ)求证:AA1⊥B1C1;
(Ⅱ)求二面角B1-AA1-C1所成角的余弦值.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得B1C1⊥A1O,AO⊥B1C1,由此能证明B1C1⊥面A1AO,从而得到B1C1⊥AA1.
(Ⅱ)过B1作B1D⊥AA1,交AA1于D,连结DC1,由已知得∠B1DC1是二面角B1-AA1-C1的平面角,由此能求出二面角B1-AA1-C1所成角的余弦值.
(Ⅱ)过B1作B1D⊥AA1,交AA1于D,连结DC1,由已知得∠B1DC1是二面角B1-AA1-C1的平面角,由此能求出二面角B1-AA1-C1所成角的余弦值.
解答:
(Ⅰ)证明:∵A在底面△A1B1C1上射影是下底面正△A1B1C1的中心O,
∴B1C1⊥A1O,又AO⊥平面A1B1C1,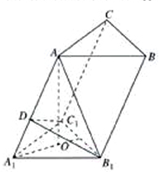
∴AO⊥B1C1,
∴B1C1和两相交直线AO,A1O均垂直,
∴B1C1⊥面A1AO,
又AA1?面A1AO,∴B1C1⊥AA1.
(Ⅱ)解:过B1作B1D⊥AA1,交AA1于D,连结DC1,
∵AA1⊥B1C1,AA1⊥DB1,
∴AA1⊥面DB1C1,∴AA1⊥DC1,
∴∠B1DC1是二面角B1-AA1-C1的平面角,
又A在底面A1B1C1上的投影是△A1B1C1的中心,
∴AA1=AB1=2a,
在△AA1B1中,由AA1=AB1=2a,A1B1=
a,
由面积法知:B1D=
=
a,同理DC1=
a,
在△C1DB1中,由余弦定理得cos∠B1DC1=
=
,
∴二面角B1-AA1-C1所成角的余弦值为
.
∴B1C1⊥A1O,又AO⊥平面A1B1C1,

∴AO⊥B1C1,
∴B1C1和两相交直线AO,A1O均垂直,
∴B1C1⊥面A1AO,
又AA1?面A1AO,∴B1C1⊥AA1.
(Ⅱ)解:过B1作B1D⊥AA1,交AA1于D,连结DC1,
∵AA1⊥B1C1,AA1⊥DB1,
∴AA1⊥面DB1C1,∴AA1⊥DC1,
∴∠B1DC1是二面角B1-AA1-C1的平面角,
又A在底面A1B1C1上的投影是△A1B1C1的中心,
∴AA1=AB1=2a,
在△AA1B1中,由AA1=AB1=2a,A1B1=
| 3 |
由面积法知:B1D=
| ||||||
| 2a |
| ||
| 4 |
| ||
| 4 |
在△C1DB1中,由余弦定理得cos∠B1DC1=
| ||||||||
2•
|
| 5 |
| 13 |
∴二面角B1-AA1-C1所成角的余弦值为
| 5 |
| 13 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
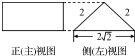 如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8
如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8| 2 |
A、2 0+8
| ||
B、2 4+8
| ||
| C、8 | ||
| D、16 |
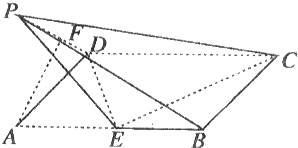
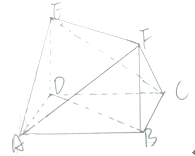 如图,多面体ABCDEF中,底面ABCD是菱形,∠BCD=60°,四边形BDEF是正方形且DE⊥平面ABCD.
如图,多面体ABCDEF中,底面ABCD是菱形,∠BCD=60°,四边形BDEF是正方形且DE⊥平面ABCD.