题目内容
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
的切线,切点为E,延长FE交双曲线右支于点P,若E为线段PF的中点,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:右焦点为F′,则PF′=a,PF=3a,EF=
a,利用勾股定理,即可求出双曲线的离心率.
| 3 |
| 2 |
解答:
解:由题意,设右焦点为F′,则PF′=a,PF=3a,
∴EF=
a,
∴c=
=
a,
∴e=
=
.
故选:C.
∴EF=
| 3 |
| 2 |
∴c=
|
| ||
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
故选:C.
点评:本题考查双曲线的离心率,考查直线与圆的位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
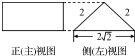 如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8
如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8| 2 |
A、2 0+8
| ||
B、2 4+8
| ||
| C、8 | ||
| D、16 |
已知直线的向量参数方程为(x,y,z)=(5,0,3)+t(0,3,0),当t=
时,则对应直线上的点的坐标是( )
| 1 |
| 2 |
| A、(5,0,3) | ||||
B、(
| ||||
C、(5,
| ||||
D、(
|
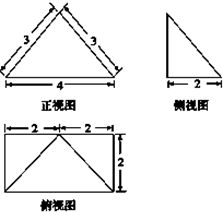 已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中的最大面积是( )
已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中的最大面积是( )| A、6 | ||
| B、8 | ||
C、2
| ||
| D、3 |
已知某几何体的三视图如图所示,则该几何体的体积是( )


A、
| ||||
B、
| ||||
C、2
| ||||
D、2
|