题目内容

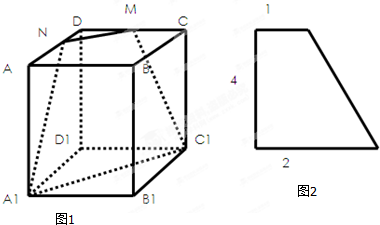
如图1所示，长方体AC1沿截面A1C1MN截得几何体DMN-D1A1C1，它的正视图、侧视图均为图2所示的直角梯形，则该几何体的体积为（　　）
A、
14
3
B、
10
3
C、14
D、10
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知可得几何体DMN-D1A1C1是三棱台，由已知中它的正视图、侧视图均为图2所示的直角梯形，代入台体体积公式可得答案．
解答： 解：由已知可得几何体DMN-D1A1C1是三棱台，
又∵它的正视图、侧视图均为图2所示的直角梯形，
故棱台的上下底面面积分别为：
1
2
和2，高为4，
故棱台的体积V=
1
3
(
1
2
+2+
2×
1
2
)×4=
14
3
，
故选：A
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
三棱锥D-ABC及其三视图中的主视图和下视图如图所示，则棱BD的长为
 
．三棱锥D-ABC的体积为
 
．
设sinβ=sinαcos（α+β），α，β∈（0，
π
2
），α+β≠
π
2
，当tanβ取得最大值时tan（α+β）的值．
已知在Rt△ABC中，其中∠A为直角，向量
OA
=
i
+
j
，
OB
=2
i
+3
j
，
OC
=（2m+1）
i
+（m-3）
j
，其中
i
，
j
是互相垂直的两个单位向量．
（1）求实数m的值；
（2）过A作AE⊥BC于E，延长AE至D，使四边形ABDC为直角梯形（其中AC、BD为底边），用
i
，
j
表示
OD
．
已知函数f（x）=lnex+1，数列{an}中，
1
e
＜a1≤1，an=
1
e
f（an-1）（n≥2），（其中e=2.71828…是自然对数的底数）．
求证：（1）f（x）≤ex；
（2）
1
e
＜an≤1；
（3）（a1-a2）a2+（a2-a3）a3+…（an-an+1）an+1＜
e2-1
2e2
．
已知a1=4，an+1=
n+2
n
an，求an．
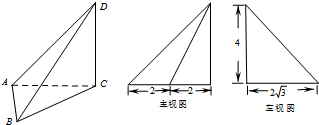
已知某几何体的三视图如图所示，则该几何体的体积是（　　）
A、
2
3
3
+π
B、
2
3
3
+2π
C、2
3
+π
D、2
3
+2π
有下列关于三角函数的命题
P1：?x∈R，x≠kπ+
π
2
（k∈Z），若tanx＞0，则sin2x＞0；
P2：函数y=sin（x-
3π
2
）与函数y=cosx的图象相同；
P3：?x0∈R，2cosx0=3；
P4：函数y=|cosx|（x∈R）的最小正周期为2π，其中真命题是（　　）
A、P1，P4
B、P2，P4
C、P2，P3
D、P1，P2
化简：
（1）5（2
a
-2
b
）+4（2
b
-3
a
）
（2）6（
a
-3
b
+
c
）-4（-
a
+
b
-
c
）
（3）
1
2
[（3
a
-2
b
）+5
a
-
1
3
（6
a
-9
b
）]
（4）（x-y）（
a
+
b
）-（x-y）（
a
-
b
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网