Question

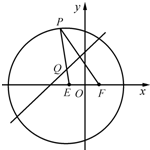如图，已知圆E：（x+1）²+y²=16，点F（1，0），P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．
（Ⅰ）求动点Q的轨迹Γ的方程；
（Ⅱ）点A（-2，0），B（2，0），点G是轨迹Γ上的一个动点，直线AG与直线x=2相交于点D，试判断以线段BD为直径的圆与直线GF的位置关系，并证明你的结论．

Answer 1

考点：轨迹方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）连结QF，根据题意，|QP|=|QF|，则|QE|+|QF|=|QE|+|QP|=4＞|EF|，故Q的轨迹Γ是以E，F为焦点，长轴长为4的椭圆，从而可求动点Q的轨迹Γ的方程；
（Ⅱ）以线段BD为直径的圆与直线GF相切，分类讨论，设直线AG的方程为y=k（x+2）（k≠0），证明圆心H到直线GF的距离d=

1

2

|BD|，即可得出结论．

解答： 解：（Ⅰ）连结QF，根据题意，|QP|=|QF|，
则|QE|+|QF|=|QE|+|QP|=4＞|EF|，
故Q的轨迹Γ是以E，F为焦点，长轴长为4的椭圆．（2分）
设其方程为

x2

a2

+

x2

b2

=1(a＞b＞0)，
可知a=2，c=

a2-b2

=1，则b=

3

，（3分）
所以点Q的轨迹Γ的方程为为

x2

4

+

y2

3

=1．（4分）
（Ⅱ）以线段BD为直径的圆与直线GF相切．（5分）
由题意，设直线AG的方程为y=k（x+2）（k≠0），则点D坐标为（2，4k），BD的中点H的坐标为（2，2k）．
联立方程组

y=k(x+2) x2 4 + y2 3 =1

消去y得（3+4k²）x²+16k²x+16k²-12=0，
设G（x₀，y₀），则-2x0=

16k2-12

3+4k2

，
所以x0=

6-8k2

3+4k2

，y0=k(x0+2)=

12k

3+4k2

，（7分）
当k=±

1

2

时，点G的坐标为(1，±

3

2

)，点D的坐标为（2，±2）．
直线GF⊥x轴，此时以BD为直径的圆（x-2）²+（y±1）²=1与直线GF相切．（9分）
当k≠±

1

2

时，则直线GF的斜率为

12k2 3+4k2

6-8k2 3+4k2 -1

=

4k

1-4k2

，则直线GF方程为y=

4k

1-4k2

(x-1)，
点H到直线GF的距离d=

| 8k 1-4k2 -2k- 4k 1-4k2 |

( 4k 1-4k2 )2+1

=

| 2k+8k3 1-4k2 |

1+4k2 |1-4k2|

=2|k|，又|BD|=4|k|，
所以圆心H到直线GF的距离d=

1

2

|BD|，此时，以BD为直径的圆与直线GF相切．
综上所述，以线段BD为直径的圆与直线GF相切．（13分）

点评：本题考查椭圆的定义与方程，考查直线与圆，直线与椭圆的位置关系，考查学生分析解决问题的能力，属于中档题．