题目内容
棱长均为3三棱锥S-ABC,若空间一点P满足
=x
+y
+z
(x+y+z=1)则|
|的最小值为( )
| SP |
| SA |
| SB |
| SC |
| SP |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
考点:向量在几何中的应用,平面向量的基本定理及其意义
专题:平面向量及应用
分析:由于空间一点P满足
=x
+y
+z
且x+y+z=1,可得点P在平面ABC内.可知:当SP⊥平面ABC,P为垂足时,|
|取得最小值.由于三棱锥S-ABC的棱长均为3,得到点P为底面ABC的中心.利用线面垂直的性质、正三角形的性质和勾股定理即可得出.
| SP |
| SA |
| SB |
| SC |
| SP |
解答:
解:∵空间一点P满足
=x
+y
+z
且x+y+z=1,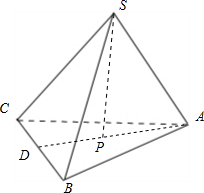
∴点P在平面ABC内.
因此当SP⊥平面ABC,P为垂足时,|
|取得最小值.
∵三棱锥S-ABC的棱长均为3,∴点P为底面ABC的中心.
∴AP=
AD,AD=
×3=
.
∴AP=
×
=
.
在Rt△APS中,SP=
=
=
.
故选:A.
| SP |
| SA |
| SB |
| SC |

∴点P在平面ABC内.
因此当SP⊥平面ABC,P为垂足时,|
| SP |
∵三棱锥S-ABC的棱长均为3,∴点P为底面ABC的中心.
∴AP=
| 2 |
| 3 |
| ||
| 2 |
3
| ||
| 2 |
∴AP=
| 2 |
| 3 |
3
| ||
| 2 |
| 3 |
在Rt△APS中,SP=
| SA2-AP2 |
32-(
|
| 6 |
故选:A.
点评:本题考查了空间向量共面定理、线面垂直的性质、正三角形的性质和勾股定理等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
设O为△ABC的外心(三角形外接圆的圆心).若
=
+
,则∠BAC的度数为( )
| AO |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| A、30° | B、45° |
| C、60° | D、90° |
设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2014)2f(x+2014)-4f(-2)>0的解集为( )
| A、(-∞,-2012) |
| B、(-2012,0) |
| C、(-∞,-2016) |
| D、(-2016,0) |
设函数f(x)=sin(2x+
),则下列结论正确的是( )
| π |
| 3 |
A、f(x)的图象关于直线x=
| ||
B、f(x)的图象关于点(
| ||
C、f(x)的最小正周期为
| ||
D、f(x)在[0,
|
某班有50名学生,其中正、副班长各1人,现要选派5人参加一项社区活动,要求正、副班长至少1人参加,问共有多少种选派方法?下面是学生提供的四个计算式,其中错误的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
将5名实习教师分配到高一年级的3个班实习,每班至少1名,则不同的分配方案有( )
| A、30种 | B、60种 |
| C、90种 | D、150种 |