题目内容
不等式x2•（x-1）＜0的解集是（ ）
| A、{x|x＞1} |
| B、{x|x＜1} |
| C、{x|0＜x＜1} |
| D、{x|x＜1，且x≠0} |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：把不等式x2•（x-1）＜0化为等价的不等式组
，求出解集即可．
|
解答：
解：不等式x2•（x-1）＜0可化为
，
解得x＜1，且x≠0；
∴不等式的解集是{x|x＜1，且x≠0}．
故选：D．
|
解得x＜1，且x≠0；
∴不等式的解集是{x|x＜1，且x≠0}．
故选：D．
点评：本题考查了不等式的解法与应用问题，解题的关键是把不等式x2•（x-1）＜0转化为等价的不等式组
，是基础题．
|
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
一枚硬币连抛2次，只有一次出现正面的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知随机变量ξ-N（μ，2），且P（ξ≥1）=
，则实数μ的值为（ ）
| 1 |
| 2 |
| A、1 | ||
B、
| ||
| C、0 | ||
| D、2 |
已知x与y之间的几组数据如下表
则y与x的线性回归方程
=bx+a必过（ ）
| x | 0 | 1 | 2 | 3 |
| y | -1 | -3 | -4 | -7 |
 |
| y |
| A、点（2，2） |
| B、点（1.5，4） |
| C、点（1.5，-3.75） |
| D、点（1.5，0） |
点M的直角坐标为（-
，-1）化为极坐标为（ ）
| 3 |
A、（2，
| ||
B、（2，
| ||
C、（2，
| ||
D、（2，
|
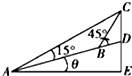如图所示，在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°，向山顶前进100米到达B处，又测得C对于山坡的斜度为45°，若CD=50米，山坡对于地平面的坡角为θ，则cosθ=（ ）A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
函数y=4x4+4x2+1的导数是（ ）
| A、16x3+4x2 |
| B、4x3+8x |
| C、16x3+8x |
| D、16x3+4x |
已知Sn是数列{an}的前n项和，Sn=an2+bn+c（a，b，c∈R），那么数列{an}（ ）
| A、不管a，b，c取何值是等差数列 |
| B、当a≠0时是等差数列 |
| C、当c=0时是等差数列 |
| D、不管a，b，c取何值都不是等差数列 |