题目内容
函数y=4x4+4x2+1的导数是（ ）
| A、16x3+4x2 |
| B、4x3+8x |
| C、16x3+8x |
| D、16x3+4x |
考点：导数的运算
专题：导数的概念及应用
分析：求函数的导数，利用导数公式即可得到结论．
解答：
解：∵f（x）=4x4+4x2+1，
∴f′（x）=16x3+8x，
故选：C
∴f′（x）=16x3+8x，
故选：C
点评：本题主要考查导数的计算，要求熟练掌握常见函数的导数公式．
练习册系列答案
相关题目
某市在一次降雨过程中，降雨量y（mm）与时间t（min）的函数关系可近似地表示为y=f（t）=
，则在时刻t=40min的降雨强度为（ ）
| 10t |
| A、20mm/min | ||
| B、400mm/min | ||
C、
| ||
D、
|
不等式x2•（x-1）＜0的解集是（ ）
| A、{x|x＞1} |
| B、{x|x＜1} |
| C、{x|0＜x＜1} |
| D、{x|x＜1，且x≠0} |
椭圆
+
=1上一点满足∠F1PF2=60°（F1，F2为焦点），则△F1PF2的面积为（ ）
| y2 |
| 25 |
| x2 |
| 9 |
| A、3 | ||||
B、3
| ||||
C、
| ||||
D、6
|
以原点为中心，焦点在y轴上的双曲线C的一个焦点为F（0，2
），一个顶点为A（0，-2），则双曲线C的方程为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
为得到函数y=sin（x+
）的图象，可将函数y=cosx的图象向右平移m（m＞0）个单位长度，则m的最小值是（ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在区间[1，3]上任取一数，则这个数大于等于1.5的概率为（ ）
| A、0.25 | B、0.5 |
| C、0.6 | D、0.75 |
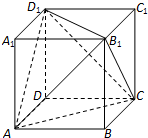如图，已知正方体ABCD-A1B1C1D1的棱长为1．