题目内容
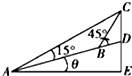 如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100米到达B处,又测得C对于山坡的斜度为45°,若CD=50米,山坡对于地平面的坡角为θ,则cosθ=( )
如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100米到达B处,又测得C对于山坡的斜度为45°,若CD=50米,山坡对于地平面的坡角为θ,则cosθ=( )A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
考点:余弦定理,正弦定理
专题:应用题,解三角形
分析:易求∠ACB=30°,在△ABC中,由正弦定理可求BC,在△BCD中,由正弦定理可求sin∠BDC,再由∠BDC=θ+90°可得答案.
解答:
解:∵∠CBD=45°,∴∠ACB=30°,
在△ABC中,由正弦定理,得
=
,即
=
,
解得BC=50(
-
),
在△BCD中,由正弦定理,得
=
,即
=
,
∴sin∠BDC=
-1,及sin(θ+90°)=
-1,
∴cosθ=
-1,
故选C.
在△ABC中,由正弦定理,得
| BC |
| sin∠CAB |
| AB |
| sin∠ACB |
| BC |
| sin15° |
| 100 |
| sin30° |
解得BC=50(
| 6 |
| 2 |
在△BCD中,由正弦定理,得
| BC |
| sin∠BDC |
| CD |
| sin∠CBD |
50(
| ||||
| sin∠BDC |
| 50 |
| sin45° |
∴sin∠BDC=
| 3 |
| 3 |
∴cosθ=
| 3 |
故选C.
点评:该题考查正弦定理在实际问题中的应用,属基础题,由实际问题恰当构建数学模型是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知cosα=-
,α∈(0,180°),则α的值是( )
| ||
| 2 |
| A、45° | B、125° |
| C、135° | D、145° |
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,则C的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| A、y=±2x | ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
已知i是虚数单位,(1+2i)z=i,则
=( )
. |
| z |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
不等式x2•(x-1)<0的解集是( )
| A、{x|x>1} |
| B、{x|x<1} |
| C、{x|0<x<1} |
| D、{x|x<1,且x≠0} |
以原点为中心,焦点在y轴上的双曲线C的一个焦点为F(0,2
),一个顶点为A(0,-2),则双曲线C的方程为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
交通局对上班、下班高峰时的车速情况作抽样调查,行驶时速(单位:km/h)的统计数据用茎叶图表示如图:
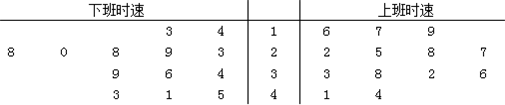
设上、下班时速的平均数分别为
上、
下,中位数分别为
上、
下,则( )

设上、下班时速的平均数分别为
. |
| x |
. |
| x |
. |
| m |
. |
| m |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|