题目内容
已知椭圆
+
=1的焦点分别是F1、F2,P是椭圆上一点,若连结F1、F2、P三点恰好能构成直角三角形,则点P到y轴的距离是( )
| x2 |
| 16 |
| y2 |
| 25 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
考点:椭圆的简单性质
专题:计算题,分类讨论,圆锥曲线的定义、性质与方程
分析:P、F1、F2是一个直角三角形的三个顶点,分两种情况:两焦点连线段F1F2为直角边;两焦点连线F1F2为斜边,计算P点纵坐标,代入方程得横坐标,即可得到P到y轴距离.
解答:
解:椭圆
+
=1的焦点在y轴上,
且为F1(0,-3),F2(0,3),
且a=5,b=4,c=3,
第一种情况,两焦点连线段F1F2为直角边,则P点纵坐标为±3,
则令y=±3,代入椭圆方程,可得,x=
P到y轴距离为
;
第二种情况,两焦点连线F1F2为斜边,
设P(x,y),则
•
=-1,即为x2+y2=9,联立椭圆方程
+
=1,则无解.
故点P到y轴的距离是
.
故选A.
| x2 |
| 16 |
| y2 |
| 25 |
且为F1(0,-3),F2(0,3),
且a=5,b=4,c=3,
第一种情况,两焦点连线段F1F2为直角边,则P点纵坐标为±3,
则令y=±3,代入椭圆方程,可得,x=
| 16 |
| 5 |
P到y轴距离为
| 16 |
| 5 |
第二种情况,两焦点连线F1F2为斜边,
设P(x,y),则
| y+3 |
| x |
| y-3 |
| x |
| x2 |
| 16 |
| y2 |
| 25 |
故点P到y轴的距离是
| 16 |
| 5 |
故选A.
点评:本题考查椭圆的标准方程,考查分类讨论的数学思想,解题的关键是正确分类,求出P点横坐标.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
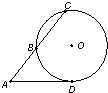 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4