题目内容
设f(x)=
,已知方程f2(x)+af(x)+b=0恰好有三个互异的实数根,求a的取值范围.
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:画出f(x)=
的图象,令t=f(x),则可将方程f2(x)+af(x)+b=0恰好有三个互异的实数根,转化为t2+at+b=0只有一个实根t0,满足t0∈(0,1),或t2+at+b=0有两个实根t1,t2,满足t0=1,t2∈(1,+∞)或t2=0,进而求出a的取值范围.
|
解答:
解:f(x)=
的图象如下图所示:
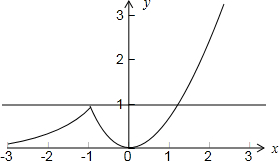 ,
,
令t=f(x),若方程f2(x)+af(x)+b=0恰好有三个互异的实数根,则:
t2+at+b=0只有一个实根t0,满足t0∈(0,1)
或t2+at+b=0有两个实根t1,t2,满足t0=1,t2∈(1,+∞)或t2=0,
若t2+at+b=0只有一个实根t0,满足t0∈(0,1),则-
∈(0,1),解得:a∈(-2,0),且a2-4b=0,
若t2+at+b=0有两个实根t1,t2,满足t0=1,t2∈(1,+∞)或t2=0,则b=0,-a∈(1,+∞),解得:a∈(-∞,-1),且b=0,
综上所述:当a2-4b=0时,a的取值范围是a∈(-2,0),
当b=0时,a的取值范围是(-∞,-1)
|
 ,
,令t=f(x),若方程f2(x)+af(x)+b=0恰好有三个互异的实数根,则:
t2+at+b=0只有一个实根t0,满足t0∈(0,1)
或t2+at+b=0有两个实根t1,t2,满足t0=1,t2∈(1,+∞)或t2=0,
若t2+at+b=0只有一个实根t0,满足t0∈(0,1),则-
| a |
| 2 |
若t2+at+b=0有两个实根t1,t2,满足t0=1,t2∈(1,+∞)或t2=0,则b=0,-a∈(1,+∞),解得:a∈(-∞,-1),且b=0,
综上所述:当a2-4b=0时,a的取值范围是a∈(-2,0),
当b=0时,a的取值范围是(-∞,-1)
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据已知中函数的解析式,画出函数的图象,再利用数形结合是解答本题的关键.

练习册系列答案
相关题目
已知椭圆
+
=1的焦点分别是F1、F2,P是椭圆上一点,若连结F1、F2、P三点恰好能构成直角三角形,则点P到y轴的距离是( )
| x2 |
| 16 |
| y2 |
| 25 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
下列命题错误的是( )
| A、命题“若x2+y2≠0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” |
| B、若命题p:?x0∈R,使得x02-x0+1≤0;则¬p:?x∈R,均有x2-x+1>0 |
| C、若p∧q为假命题,则p∨¬q为真命题 |
| D、“x>|y|”是“x2>y2”的充分不必要条件 |