题目内容
长方体ABCD-A1B1C1D1的各顶点都在以O为球心的球面上,且AB=AD=1,AA1=
,则A、D1两点的球面距离为 .
| 2 |
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:可先利用长方体三边长求出球半径,在三角形中求出球心角,再利用球面距离公式得出答案.
解答:
解:设A、D1两点在该球面上的球面距离为d,球的直径即为长方体的对角线长,
即球半径R满足2R=
=2,
∴R=1,
在三角形OAD1中,OA=OD1=1,AD1=
,球心角∠AOD1=
,
∴利用球面距离公式得出:d=α•R=
•1=
,
故答案为:
.
即球半径R满足2R=
| 1+1+2 |
∴R=1,
在三角形OAD1中,OA=OD1=1,AD1=
| 3 |
| 2π |
| 3 |
∴利用球面距离公式得出:d=α•R=
| 2π |
| 3 |
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题主要考查球的性质、球内接多面体、球面距离,属于基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知椭圆
+
=1的焦点分别是F1、F2,P是椭圆上一点,若连结F1、F2、P三点恰好能构成直角三角形,则点P到y轴的距离是( )
| x2 |
| 16 |
| y2 |
| 25 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
已知f(x)是定义在[a,b]上的函数,其图象是一条连续的曲线,且满足下列条件:
①f(x)的值域为M,且M⊆[a,b];
②对任意不相等的x,y∈[a,b],都有|f(x)-f(y)|<|x-y|.
那么,关于x的方程f(x)=x在区间[a,b]上根的情况是( )
①f(x)的值域为M,且M⊆[a,b];
②对任意不相等的x,y∈[a,b],都有|f(x)-f(y)|<|x-y|.
那么,关于x的方程f(x)=x在区间[a,b]上根的情况是( )
| A、没有实数根 |
| B、有且仅有一个实数根 |
| C、恰有两个不等的实数根 |
| D、实数根的个数无法确定 |
下列命题错误的是( )
| A、命题“若x2+y2≠0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” |
| B、若命题p:?x0∈R,使得x02-x0+1≤0;则¬p:?x∈R,均有x2-x+1>0 |
| C、若p∧q为假命题,则p∨¬q为真命题 |
| D、“x>|y|”是“x2>y2”的充分不必要条件 |
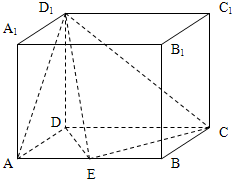 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,