题目内容
设曲线y=3x2与x轴以及直线x=2围成的封闭图形的面积为a,函数f(x)=2|x+1|+|x-1|,则使f(x)≥a成立的x取值范围是 .
考点:定积分在求面积中的应用
专题:导数的综合应用
分析:首利用定积分的几何意义求出a,然后数形结合求a的范围.
解答:
解:由题意,a=
3x2dx=x3|
=8,
函数f(x)=2|x+1|+|x-1|,=的图象如下,

2|x+1|+|x-1|=8,解得|x+1|+|x-1|=3,解得x=
或x=-
,
所以使f(x)≥a成立的x取值范围是(-∞,-
]∪[
,+∞).
故答案为:(-∞,-
]∪[
,+∞).
| ∫ | 2 0 |
2 0 |
函数f(x)=2|x+1|+|x-1|,=的图象如下,

2|x+1|+|x-1|=8,解得|x+1|+|x-1|=3,解得x=
| 3 |
| 2 |
| 3 |
| 2 |
所以使f(x)≥a成立的x取值范围是(-∞,-
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:(-∞,-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了利用定积分求曲边梯形的面积以及数形结合求不等式成立的参数范围,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知椭圆
+
=1的焦点分别是F1、F2,P是椭圆上一点,若连结F1、F2、P三点恰好能构成直角三角形,则点P到y轴的距离是( )
| x2 |
| 16 |
| y2 |
| 25 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
下列命题错误的是( )
| A、命题“若x2+y2≠0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” |
| B、若命题p:?x0∈R,使得x02-x0+1≤0;则¬p:?x∈R,均有x2-x+1>0 |
| C、若p∧q为假命题,则p∨¬q为真命题 |
| D、“x>|y|”是“x2>y2”的充分不必要条件 |
已知平面向量
,
满足|
|=
,|
|=2,且(
-
)⊥
,则
与
的夹角为( )
| a |
| b |
| a |
| 3 |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
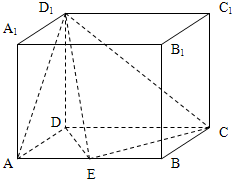 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,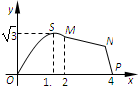 如图,某市拟在长为4km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),X∈[0,2]的图象,且图象的最高点为S(
如图,某市拟在长为4km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),X∈[0,2]的图象,且图象的最高点为S(