题目内容
已知函数f(x)=ax+x2-xlna,a>1.
(Ⅰ)求证:函数f(x)在(0,+∞)上单调递增;
(Ⅱ)若方程|f(x)-t|=1有三个不同的实根,求t的值;
(Ⅲ)对任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1恒成立,求a的取值范围.
(Ⅰ)求证:函数f(x)在(0,+∞)上单调递增;
(Ⅱ)若方程|f(x)-t|=1有三个不同的实根,求t的值;
(Ⅲ)对任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1恒成立,求a的取值范围.
考点:利用导数研究函数的单调性,函数的零点与方程根的关系,导数在最大值、最小值问题中的应用
专题:函数的性质及应用
分析:(Ⅰ)证明a>1时函数的导数大于0.
(Ⅱ)先判断函数f(x)的极小值,再由y=|f(x)-t|-1有三个零点,所以方程f(x)=t±1有三个根,根据t-1应是f(x)的极小值,解出t.
(Ⅲ)f(x)的最大值减去f(x)的最小值大于或等于e-1,由单调性知,f(x)的最大值是f(1)或f(-1),最小值f(0)=1,由f(1)-f(-1)的单调性,判断f(1)与f(-1)的大小关系,再由f(x)的最大值减去最小值f(0)大于或等于e-1求出a的取值范围.
(Ⅱ)先判断函数f(x)的极小值,再由y=|f(x)-t|-1有三个零点,所以方程f(x)=t±1有三个根,根据t-1应是f(x)的极小值,解出t.
(Ⅲ)f(x)的最大值减去f(x)的最小值大于或等于e-1,由单调性知,f(x)的最大值是f(1)或f(-1),最小值f(0)=1,由f(1)-f(-1)的单调性,判断f(1)与f(-1)的大小关系,再由f(x)的最大值减去最小值f(0)大于或等于e-1求出a的取值范围.
解答:
解:(I)f′(x)=axlna+2x-lna=2x+(ax-1)lna,…(2分)
由于a>1,故当x∈(0,+∞)时,lna>0,ax-1>0,所以f′(x)>0,
所以函数f(x)在(0,+∞)上单调递增; …(4分)
(II)令f′(x)=2x+(ax-1)lna=0,解得x=0,…(5分)
x,f(x),f′(x)的变化情况表如下:
因为方程|f(x)-t|=1有三个不同的实根,所以f(x)=t±1
故当x→∞时,f(x)→+∞,
t-1=f(x)min=f(0)=,所以t=2;…(8分)
(III)由(II)可知f(x)在区间[-1,0]单调递减,在[0,1]单调递增.
所以f(x)min=f(0)=1,f(x)max=max{f(-1),f(1)},f(-1)=
+1+lna,f(1)=a+1-lna,
f(1)-f(-1)=a-
-2lna,
设函数g(x)=x-
-2lnx,g′(x)=1+
-
=(
-1)2,所以g′(x)≥0(当x=1时取等号)
所以g(x)=x-
-2lnx递增,g(1)=0,a>1,
所以f(1)-f(-1)=a-
-2lna>0,
所以f(1)>f(-1)…(11分)
对任意x1,x2∈[-1,1],|f(x1)-f(x2)|max=|f(1)-f(0)|=a-lna≤e-1,
所以1<a≤e.
由于a>1,故当x∈(0,+∞)时,lna>0,ax-1>0,所以f′(x)>0,
所以函数f(x)在(0,+∞)上单调递增; …(4分)
(II)令f′(x)=2x+(ax-1)lna=0,解得x=0,…(5分)
x,f(x),f′(x)的变化情况表如下:
| x | (-∞,0) | 0 | (0,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
故当x→∞时,f(x)→+∞,
t-1=f(x)min=f(0)=,所以t=2;…(8分)
(III)由(II)可知f(x)在区间[-1,0]单调递减,在[0,1]单调递增.
所以f(x)min=f(0)=1,f(x)max=max{f(-1),f(1)},f(-1)=
| 1 |
| a |
f(1)-f(-1)=a-
| 1 |
| a |
设函数g(x)=x-
| 1 |
| x |
| 1 |
| x2 |
| 2 |
| x |
| 1 |
| x |
所以g(x)=x-
| 1 |
| x |
所以f(1)-f(-1)=a-
| 1 |
| a |
所以f(1)>f(-1)…(11分)
对任意x1,x2∈[-1,1],|f(x1)-f(x2)|max=|f(1)-f(0)|=a-lna≤e-1,
所以1<a≤e.
点评:本题考查函数的零点,用导数判断函数单调性,利用导数研究函数极值,属于难题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
设点P是不等式
表示的平面区域内D内的一点,点Q是圆C1:x2+y2-8x+2y+12+m=0上的一点,且平面区域D在圆C外,若线段PQ长的最大值小于3
,最小值大于
,则实数m的取值范围( )
|
| 5 |
| ||
| 2 |
| A、(-1,1) | ||
B、(
| ||
C、(
| ||
D、(
|
已知椭圆
+
=1的焦点分别是F1、F2,P是椭圆上一点,若连结F1、F2、P三点恰好能构成直角三角形,则点P到y轴的距离是( )
| x2 |
| 16 |
| y2 |
| 25 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
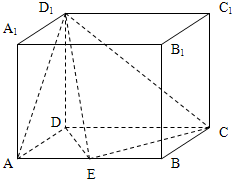 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,