题目内容
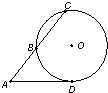 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4| 3 |
考点:与圆有关的比例线段
专题:立体几何
分析:要求圆心O到AC的距离,我们要先做出O点到AC的垂线段OE,则OE的长度即为所求,根据半径、半弦长(BE)、弦心距(OE)构成直角三角形,满足勾股定理,故我们要要求出半弦长(BE),根据切割线定理,我可以求出AB长,进而得到BE,代入即可得到答案.
解答:
解:连接OB,过O点向AC引垂线,垂足为E,

∵AD=4
,AC=12,由切割线定理可得,
AD2=AC•AB,
∴AB=4,
∴BC=8,
由垂径定理得BE=4.
又∵R=OB=5,
∴OE=
=3,
故答案为:3.

∵AD=4
| 3 |
AD2=AC•AB,
∴AB=4,
∴BC=8,
由垂径定理得BE=4.
又∵R=OB=5,
∴OE=
| 52-42 |
故答案为:3.
点评:要求圆到割线的距离,即弦心距,我们最常用的性质是:半径、半弦长(BE)、弦心距(OE)构成直角三角形,满足勾股定理,求出半径和半弦长,代入即可求解.

练习册系列答案
相关题目
已知椭圆
+
=1的焦点分别是F1、F2,P是椭圆上一点,若连结F1、F2、P三点恰好能构成直角三角形,则点P到y轴的距离是( )
| x2 |
| 16 |
| y2 |
| 25 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
已知某算法的流程图如图所示,则程序运行结束时输出的结果为( )

| A、10 | B、19 |
| C、-10 | D、-19 |
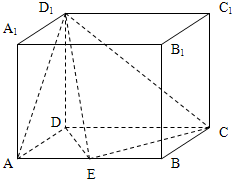 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,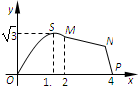 如图,某市拟在长为4km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),X∈[0,2]的图象,且图象的最高点为S(
如图,某市拟在长为4km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),X∈[0,2]的图象,且图象的最高点为S(