Question

在平面直角坐标系中，设点P（x，y），定义[OP]=|x|+|y|，其中O为坐标原点．对于下列结论：
（1）符合[OP]=1的点P的轨迹围成的图形的面积为2；
（2）设点P是直线：

5

x+2y-2=0上任意一点，则[OP]_min=

2 5

5

；
（3）设点P是直线：y=kx+1（k∈R）上任意一点，则“使得[OP]最小的点P有无数个”的充要条件是“k=±1”；
（4）设点P是椭圆

x2

4

+y²=1上任意一点，则[OP]_max=5．
其中正确的结论序号为（　　）

• A、（1）、（2）、（3）
• B、（1）、（3）、（4）
• C、（2）、（3）、（4）
• D、（1）、（2）、（4）

Answer 1

考点：命题的真假判断与应用

专题：新定义,简易逻辑

分析：（1）根据新定义由[OP]=|x|+|y|=1，讨论x的取值，得到y与x的分段函数关系式，画出分段函数的图象，由图象可知点P的轨迹围成的图形为边长是

2

的正方形，求出正方形的面积即可；
（2）把[OP]=|x|+|y|转化为仅含x的表达式，求出x的范围，利用一次函数的单调性即可得到[OP]的最小值为

2 5

5

；
（3）根据|x|+|y|大于等于|x+y|或|x-y|，把y=kx+1代入即可得到当[OP]最小的点P有无数个时，k等于1或-1；而k等于1或-1推出[OP]最小的点P有无数个，得到k=±1是“使[OP]最小的点P有无数个”的充要条件；
（4）把P的坐标用参数表示，然后利用三角函数的化积求得[OP]=|x|+|y|的最大值说明命题错误．

解答： 解：（1）由[OP]=1，根据新定义得：|x|+|y|=1，
可化为：

y=-x+1，0≤x≤1，0≤y≤1 y=x-1，0≤x≤1，-1≤y≤0 y=x+1，-1≤x≤0，0≤y≤1 y=-x-1，-1≤x≤0，-1≤y≤0

，
画出图象如图所示：

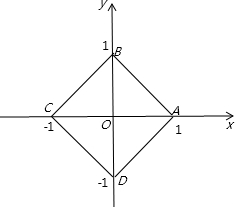
根据图形得到：四边形ABCD为边长是

2

的正方形，面积等于2，（1）正确；
（2）∵点P是直线：

5

x+2y-2=0上任意一点，则y=-

5

2

x+1，
[OP]=|x|+|y|=x-

5

2

x+1（0≤x≤

2 5

5

），当x=

2 5

5

时[OP]_min=

2 5

5

，（2）正确；
（3）∵|x|+|y|≥|x+y|=|（k+1）x+1|，当k=-1时，|x|+|y|≥|1|=1，满足题意；
而|x|+|y|≥|x-y|=|（k-1）x-1|，当k=1时，|x|+|y|≥|-1|=1，满足题意．
∴“使[OP]最小的点P有无数个”的充要条件是“k=±1”，（3）正确；
（4）∵点P是椭圆

x2

4

+y²=1上任意一点，则可设

x=2cosθ y=sinθ

，
[OP]=|x|+|y|=2cosθ+sinθ=

5

sin(θ+φ)，（θ∈[0，

π

2

]，tanφ=2），
∴[OP]_max=

5

，（4）错误．
则正确的结论有：（1）、（2）、（3）．
故选：A．

点评：此题考查学生理解及运用新定义的能力，考查了数形结合的数学思想，关键是对题意的理解，是中档题．