题目内容
19.2月21日教育部举行新闻发布会,介绍2017年全国靑少年校园足球工作计划,提出将着力提高校园足球特色学校的建设质量和水平,争取提前完成建设2万所校园足球特色学校,到2025年校园足球特色学校将达到5万所.为了调查学生喜欢足球是否与性别有关,从某足球特色学校抽取了50名同学进行调查,得到以下数据(单位:人):| 喜爱 | 不喜爱 | 合计 | |
| 男同学 | 24 | 6 | 30 |
| 女同学 | 6 | 14 | 20 |
| 合计 | 30 | 20 | 50 |
(2)现从30个喜爱足球的同学中按分层抽样的方法抽出5人,再从里面任意选出2人对其训练情况进行全程跟踪调查,求选出的刚好是一男一女的概率.
附表及公式:
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
分析 (1)由表中数据计算得K2,对照临界值得出结论;
(2)用列举法求出基本事件数,计算所求的概率值.
解答 解:(1)由表中数据计算得K2的观测值为
${K^2}=\frac{{50×{{({24×14-6×6})}^2}}}{30×20×30×20}=\frac{25}{2}=12.5>10.828$,
所以在犯错概率不超过0.001的前提下认为喜爱足球与性別有关;
(2)从30个喜爱足球的同学中按分层抽样的方法抽出5人,
则有4名男生,1名女生,记4个男同学为,a,b,c,d;
女同学为A,从中再任意选出2人,则所有选法是
(a,b),(a,c),(a,d),(a,A),(b,c),
(b,d),(b,A),(c,d),(c,A),(d,A)共10种,
刚好是一男一女的情况有4种,
故所求的概率为$P=\frac{4}{10}=\frac{2}{5}$.
点评 本题考查了独立性检验与列举法求古典概型的概率问题,是基础题.

练习册系列答案
相关题目
9.焦点在y轴上的双曲线的一条渐近线方程为$y=\frac{3}{4}x$,则该双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3\sqrt{7}}{7}$ |
10.设复数z的共轭复数为$\overline z$,满足z+$\overline z=z•\overline z=2$,则${({\frac{\overline z}{z}})^{2017}}$=( )
| A. | ±i | B. | i | C. | -i | D. | 1 |
7.复数z满足$\frac{1+i}{z}=\frac{i}{1+2i}(i$为虚数单位),则z=( )
| A. | 3+i | B. | 3-i | C. | -3+i | D. | -3-i |
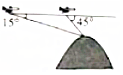 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,则山顶的海拔高度为(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$)( )
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,则山顶的海拔高度为(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$)( )