题目内容
4.已知等比数列{an}的前n项和为Sn,公比为$\frac{3}{2}$.(1)若${S_4}=\frac{65}{24}$,求a1;
(2)若a1=2,${c_n}=\frac{1}{2}{a_n}+bn$,且c2,c4,c5成等差数列,求b.
分析 (1)利用等比数列的公比,结合${S_4}=\frac{65}{24}$,直接求解a1;
(2)通过a1=2,化简${c_n}=\frac{1}{2}{a_n}+bn$,利用c2,c4,c5成等差数列,得到方程,求解b即可.
解答 解:(1)∵公比$q=\frac{3}{2}$,${S_4}=\frac{65}{24}$,
∴$\frac{{{a_1}[1-{{(\frac{3}{2})}^4}]}}{{1-\frac{3}{2}}}=\frac{65}{24}$,
则$(1-\frac{81}{16}){a_1}=-\frac{65}{48}$,
解得${a_1}=\frac{1}{3}$.
(2)∵a1=2,公比为$\frac{3}{2}$,∴a2=3,${a_4}=\frac{27}{4}$,${a_5}=\frac{81}{8}$,
∴${c_2}=\frac{3}{2}+2b$,${c_4}=\frac{27}{8}+4b$,${c_5}=\frac{81}{16}+5b$.
∵c2,c4,c5成等差数列.
∴$2(\frac{27}{8}+4b)=\frac{3}{2}+2b+\frac{81}{16}+5b$.
解得$b=-\frac{3}{16}$.
点评 本题考查数列的递推关系式的应用,考查转化思想以及计算能力.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
15.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的两个焦点,M(x0,y0)(x0>0,y0>0)是双曲线的渐近线上一点,满足MF1⊥MF2,如果以F2为焦点的抛物线y2=2px(p>0)经过点M,则此双曲线的离心率为( )
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
12.某高校大一新生的五名同学打算参加学校组织的“小草文学社”、“街舞俱乐部”、“足球之家”、“骑行者”四个社团.若毎个社团至少一名同学参加,每名同学至少参加一个社团且只能参加一个社团,其中同学甲不参加“街舞俱乐部”,则这五名同学不同的参加方法的种数为( )
| A. | 160 | B. | 180 | C. | 200 | D. | 220 |
19.2月21日教育部举行新闻发布会,介绍2017年全国靑少年校园足球工作计划,提出将着力提高校园足球特色学校的建设质量和水平,争取提前完成建设2万所校园足球特色学校,到2025年校园足球特色学校将达到5万所.为了调查学生喜欢足球是否与性别有关,从某足球特色学校抽取了50名同学进行调查,得到以下数据(单位:人):
(1)能否在犯错概率不超过0.001的前提下认为喜爱足球与性别有关?
(2)现从30个喜爱足球的同学中按分层抽样的方法抽出5人,再从里面任意选出2人对其训练情况进行全程跟踪调查,求选出的刚好是一男一女的概率.
附表及公式:
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 喜爱 | 不喜爱 | 合计 | |
| 男同学 | 24 | 6 | 30 |
| 女同学 | 6 | 14 | 20 |
| 合计 | 30 | 20 | 50 |
(2)现从30个喜爱足球的同学中按分层抽样的方法抽出5人,再从里面任意选出2人对其训练情况进行全程跟踪调查,求选出的刚好是一男一女的概率.
附表及公式:
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
2.已知函数f(x)的图象关于(1,1)对称,当x∈(0,1]时,f(x)=x2,当x∈(-1,0]时,f(x)+2=$\frac{2}{f(\sqrt{x+1})}$,若g(x)=f(x)-t(x+1)为定义在(-1,3)上的函数,则关于g(x)的零点个数的叙述中错误的是( )
| A. | g(x)可能没有零点 | B. | g(x)可能有1个零点 | C. | g(x)可能有2个零点 | D. | g(x)可能有3个零点 |
6.有4个不同的球,四个不同的盒子,把球全部放入盒内,恰有两个盒不放球,共有( )种放法.
| A. | 114 | B. | 96 | C. | 84 | D. | 48 |
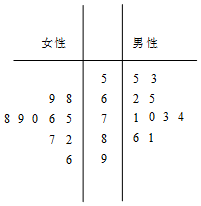 某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示: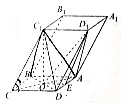 如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.
如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.