题目内容
4.已知α∈(0,$\frac{π}{2}$),试比较α,sinα,tanα的大小.分析 由题意作出三角函数线,通过三角形的面积以及扇形面积的大小比较可得.
解答 解:在直角坐标系中结合单位圆作出锐角α的正弦线和正切线,
如图所示;
由图可知sinα=MP,α=$\widehat{AP}$,tanα=AT,
∵S△AOP=$\frac{1}{2}$×MP×1=$\frac{1}{2}$sinα,
S扇形AOP=$\frac{1}{2}$×$\widehat{AP}$×1=$\frac{1}{2}$α,
S△AOT=$\frac{1}{2}$×AT×1=$\frac{1}{2}$tanα,
且S△AOP<S扇形AOP<S△AOT,
∴MP<$\widehat{AP}$<AT,
即sinα<α<tanα.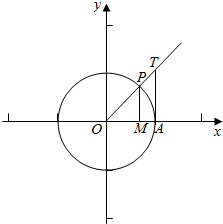
点评 本题考查了三角函数线,也考查了数形结合与转化思想应用问题,属中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
2.已知集合M={(x,y)||x|+|y|≤1},若实数对(λ,μ)满足:对任意的(x,y)∈M,都有(λx,μy)∈M,则称(λ,μ)是集合M的“嵌入实数对”.则以下集合中,不存在集合M的“嵌入实数对”的是( )
| A. | {(λ,μ)|λ-μ=2} | B. | {(λ,μ)|λ+μ=2} | C. | {(λ,μ)|λ2-μ2=2} | D. | {(λ,μ)|λ2+μ2=2} |
19.2月21日教育部举行新闻发布会,介绍2017年全国靑少年校园足球工作计划,提出将着力提高校园足球特色学校的建设质量和水平,争取提前完成建设2万所校园足球特色学校,到2025年校园足球特色学校将达到5万所.为了调查学生喜欢足球是否与性别有关,从某足球特色学校抽取了50名同学进行调查,得到以下数据(单位:人):
(1)能否在犯错概率不超过0.001的前提下认为喜爱足球与性别有关?
(2)现从30个喜爱足球的同学中按分层抽样的方法抽出5人,再从里面任意选出2人对其训练情况进行全程跟踪调查,求选出的刚好是一男一女的概率.
附表及公式:
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 喜爱 | 不喜爱 | 合计 | |
| 男同学 | 24 | 6 | 30 |
| 女同学 | 6 | 14 | 20 |
| 合计 | 30 | 20 | 50 |
(2)现从30个喜爱足球的同学中按分层抽样的方法抽出5人,再从里面任意选出2人对其训练情况进行全程跟踪调查,求选出的刚好是一男一女的概率.
附表及公式:
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
16.设非零向量$\overrightarrow{a}$=(x,2x),$\overrightarrow{b}$=(-3x,2),且$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为钝角,则x的取值范围是( )
| A. | (-∞,0) | B. | ($\frac{4}{3}$,0) | ||
| C. | (-∞,0)∪($\frac{4}{3}$,0) | D. | (-∞,-$\frac{1}{3}$)∪(-$\frac{1}{3}$,0)∪($\frac{4}{3}$,+∞) |
13.设全集U={1,2,3,4,5},∁U(A∪B)={1},A∩(∁UB)={3,4},则集合B=( )
| A. | {1,2,4,5} | B. | {2,4,5} | C. | {1,2,5} | D. | {2,5} |
14.已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-$\frac{π}{2}$≤φ<$\frac{π}{2}$)的图象关于直线x=$\frac{π}{3}$对称,且图象上相邻最高点的距离为π.将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位后,得到y=g(x)的图象,则g(x)的单调递减区间为.
| A. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | B. | [kπ-$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z | ||
| C. | [kπ-$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | D. | [kπ+$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z |
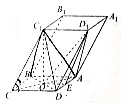 如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.
如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.