题目内容
如图，正方体ABCD-EFGH中，O为侧面ADHE的中点，求：（1）BE与CG所成的角；
（2）FO与BD所成的角．
考点：异面直线及其所成的角
专题：计算题,空间角
分析：（1）由CG∥BF，可得∠EBF（或其补角）为异面直线BE与CG所成的角；
（2）证明四边形HFBD为平行四边形，可得HF∥BD，从而∠HFO（或其补角）为异面直线FO与BD所成的角．
（2）证明四边形HFBD为平行四边形，可得HF∥BD，从而∠HFO（或其补角）为异面直线FO与BD所成的角．
解答：
解：（1）∵CG∥BF，∴∠EBF（或其补角）为异面直线BE与CG所成的角，又△BEF中，∠EBF=45°，∴BE与CG所成的角为45°；
（2）连结FH，
∵HD∥FB，HD=FB，
∴四边形HFBD为平行四边形，∴HF∥BD，
∴∠HFO（或其补角）为异面直线FO与BD所成的角．
连结HA、AF，易得FH=HA=AF，∴△AFH为等边三角形，
又依题意知O为AH中点，∴∠HFO=30°，即FO与BD所成的夹角是30°．
（2）连结FH，
∵HD∥FB，HD=FB，
∴四边形HFBD为平行四边形，∴HF∥BD，
∴∠HFO（或其补角）为异面直线FO与BD所成的角．
连结HA、AF，易得FH=HA=AF，∴△AFH为等边三角形，
又依题意知O为AH中点，∴∠HFO=30°，即FO与BD所成的夹角是30°．
点评：本题考查异面直线所成的角，考查学生的计算能力，确定异面直线所成的角是关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
函数y=x2+x+1在[-1，1]上的最小值和最大值分别是（ ）
| A、1，3 | ||
B、
| ||
C、-
| ||
D、-
|
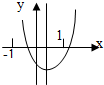已知二次函数f（x）=ax2+bx+c（a≠0）的图象如图所示，设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b，则（ ）| A、M＞0 | B、M≥0 |
| C、M＜0 | D、M=0 |
已知函数f（x）≠1，且对定义域内任意x总有关系[f（x+π）+1]•[f（x）+1]=2，那么下列结论中正确的是（ ）
| A、f（x）是周期为π的周期函数 | ||
| B、f（x）是周期为2π的周期函数 | ||
C、f（x）是周期为
| ||
| D、f（x）不是周期函数 |