题目内容
求半径为10,且与直线4x+3y-70=0相切于点A(10,10)的圆的方程.
考点:圆的一般方程
专题:直线与圆
分析:设圆心坐标为(a,b),利用半径为10,且与直线4x+3y-70=0切于点A(10,10),建立方程组,求出圆心坐标,即可求得圆的方程.
解答:
解:设要求的圆心的坐标为C(a,b),则由
,求得
,或
,
∴要求的圆的方程为(x-18)2+(y-16)2=100,或(x-2)2+(y-4)2=100.
|
|
|
∴要求的圆的方程为(x-18)2+(y-16)2=100,或(x-2)2+(y-4)2=100.
点评:本题主要考查求圆的标准方程的方法,求出圆心坐标,是解题的关键,属于基础题.

练习册系列答案
相关题目
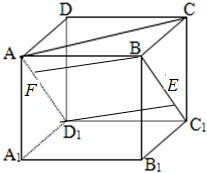 如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少?
如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少? 如图,正方体ABCD-EFGH中,O为侧面ADHE的中点,求:
如图,正方体ABCD-EFGH中,O为侧面ADHE的中点,求: