题目内容
6.已知椭圆$E:\frac{x^2}{4}+{y^2}=1$的左右顶点分别为A,B,点P为椭圆上异于A,B的任意一点.(Ⅰ)求直线PA与PB的斜率之积;
(Ⅱ)过点Q(-1,0)作与x轴不重合的直线交椭圆E于M,N两点.问:是否存在以MN为直径的圆经过点A,若存在,请求出直线MN.若不存在,请说明理由.
分析 (Ⅰ)由已知椭圆方程可得A,B的坐标,设出P点坐标,写出直线PA与PB的斜率之积,结合P在椭圆上可得答案;
(Ⅱ)设出MN所在直线方程,联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系结合平面向量数量积不为0,说明不存在以MN为直径的圆经过点A.
解答 解:(Ⅰ)由椭圆方程可知A(-2,0),B(2,0),
设P(x0,y0),则${{y}_{0}}^{2}=1-\frac{{{x}_{0}}^{2}}{4}$,
∴${k_{PA}}•{k_{PB}}=\frac{y_0}{{{x_0}+2}}•\frac{y_0}{{{x_0}-2}}=\frac{y_0^2}{x_0^2-4}=\frac{{1-\frac{x_0^2}{4}}}{x_0^2-4}=-\frac{1}{4}$;
(Ⅱ)不存在以MN为直径的圆经过点A.
事实上,设直线MN方程为:x=ty-1,
联立$\left\{\begin{array}{l}x=ty-1\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.⇒({{t^2}+4}){y^2}-2ty-3=0$,
设交点M(x1,y1),N(x2,y2),
则${y_1}+{y_2}=\frac{2t}{{{t^2}+4}},{y_1}{y_2}=\frac{-3}{{{t^2}+4}}$,
若存在以MN为直径的圆经过点A,
则$\overrightarrow{AM}•\overrightarrow{AN}=({{x_1}+2,{y_1}})•({{x_2}+2,{y_2}})$
=$({{x_1}+2})•({{x_2}+2})+{y_1}{y_2}=({t{y_1}+1})•({t{y_2}+1})+{y_1}{y_2}=({{t^2}+1}){y_1}{y_2}+t({{y_1}+{y_2}})+1$
=$\frac{{-3({{t^2}+1})}}{{{t^2}+4}}+\frac{{2{t^2}}}{{{t^2}+4}}+1=\frac{1}{{{t^2}+4}}=0$,
该方程无解,∴不存在以MN为直径的圆经过点A.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案南山一棵竹,竹尾风割断,剩下三十节,一节一个圈.头节高五寸①,头圈一尺三②.
逐节多三分③,逐圈少分三④.一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是多远?
此民谣提出的问题的答案是( )
(注:①五寸即0.5尺.②一尺三即1.3尺.③三分即0.03尺.④分三即一分三厘,等于0.013尺.)
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 6条 |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | {x|x<0,或x>2} | B. | {x|0<x<2} | C. | {x|0≤x<1} | D. | {x|0≤x≤1} |
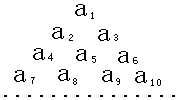 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.